Question

Area bounded by $C_1$: $y^3 = ax^2$, $C_2$: $y^2 = \frac{3-x}{x+a}$ and x-axis ($a \in N$) is/are

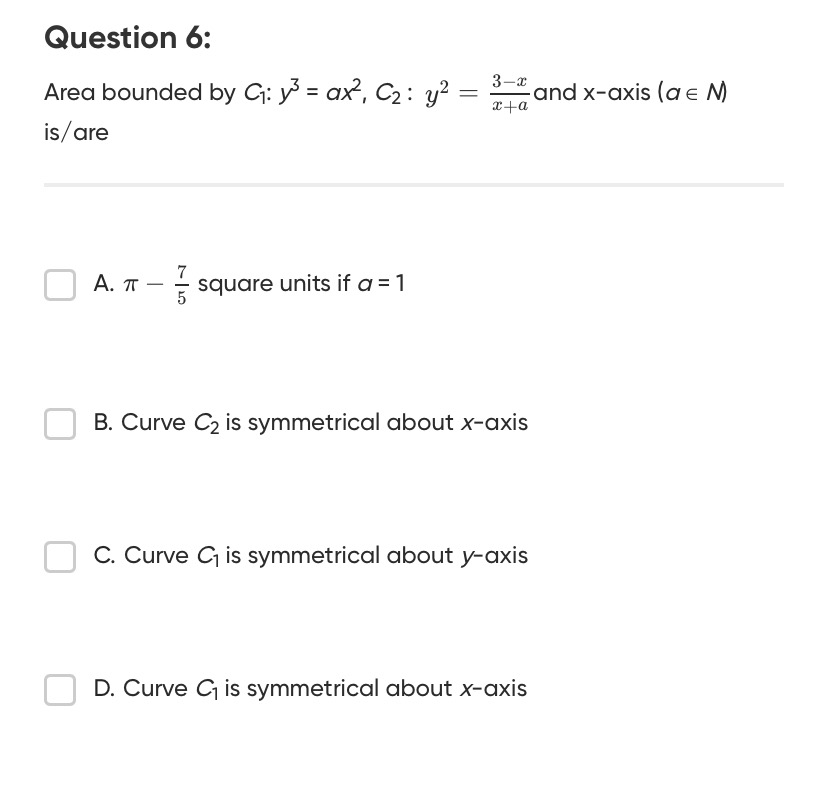
• A. $\pi - \frac{7}{5}$ square units if $a = 1$
• B. Curve $C_2$ is symmetrical about x-axis
• C. Curve $C_1$ is symmetrical about y-axis
• D. Curve $C_1$ is symmetrical about x-axis

Answer 1

Answer: (A), (B), (C)

A, B, C

Answer 2

The problem asks us to analyze the properties of two curves $C_1: y^3 = ax^2$ and $C_2: y^2 = \frac{3-x}{x+a}$ (where $a \in \mathbb{N}$), and to calculate the area bounded by them and the x-axis for $a=1$.

Let's analyze each option:

Option B: Curve $C_2$ is symmetrical about x-axis

The equation of $C_2$ is $y^2 = \frac{3-x}{x+a}$. To check for symmetry about the x-axis, we replace $y$ with $-y$ in the equation. $(-y)^2 = \frac{3-x}{x+a}$ $y^2 = \frac{3-x}{x+a}$ Since the equation remains unchanged, curve $C_2$ is symmetrical about the x-axis. Therefore, Option B is correct.

Option C: Curve $C_1$ is symmetrical about y-axis

The equation of $C_1$ is $y^3 = ax^2$. To check for symmetry about the y-axis, we replace $x$ with $-x$ in the equation. $y^3 = a(-x)^2$ $y^3 = ax^2$ Since the equation remains unchanged, curve $C_1$ is symmetrical about the y-axis. Therefore, Option C is correct.

Option D: Curve $C_1$ is symmetrical about x-axis

The equation of $C_1$ is $y^3 = ax^2$. To check for symmetry about the x-axis, we replace $y$ with $-y$ in the equation. $(-y)^3 = ax^2$ $-y^3 = ax^2$ This is not the original equation $y^3 = ax^2$ (unless $ax^2=0$, which is not generally true). Therefore, curve $C_1$ is not symmetrical about the x-axis. Option D is incorrect.

Option A: $\pi - \frac{7}{5}$ square units if $a = 1$

We need to find the area bounded by $C_1: y^3 = x^2$ (for $a=1$), $C_2: y^2 = \frac{3-x}{x+1}$ (for $a=1$) and the x-axis.

First, let's determine the relevant parts of the curves. For $C_1: y^3 = x^2 \implies y = x^{2/3}$. Since $x^2 \ge 0$, $y^3 \ge 0$, so $y \ge 0$. This part of the curve lies above or on the x-axis. It passes through $(0,0)$. For $C_2: y^2 = \frac{3-x}{x+1}$. For the curve to be real, $\frac{3-x}{x+1} \ge 0$. This inequality holds for $x \in (-1, 3]$. Since we are looking for the area bounded by the x-axis, we consider $y \ge 0$, so $y = \sqrt{\frac{3-x}{x+1}}$. This curve passes through $(3,0)$ (when $x=3, y=0$). As $x \to -1^+$, $y \to \infty$.

Next, find the intersection points of $C_1$ and $C_2$ (for $y \ge 0$). $y = x^{2/3}$ and $y = \sqrt{\frac{3-x}{x+1}}$. Equating $y^2$ from both equations: $(x^{2/3})^2 = \frac{3-x}{x+1} \implies x^{4/3} = \frac{3-x}{x+1}$. By inspection, let's try $x=1$: $1^{4/3} = \frac{3-1}{1+1} \implies 1 = \frac{2}{2} \implies 1=1$. So, $x=1$ is an intersection point. When $x=1$, $y = 1^{2/3} = 1$. Thus, $(1,1)$ is the intersection point.

The area bounded by $C_1$, $C_2$ and the x-axis is composed of two parts:

1. The area under $C_1$ from $x=0$ to $x=1$. Let this be $A_1$.
2. The area under $C_2$ from $x=1$ to $x=3$. Let this be $A_2$.

$A_1 = \int_0^1 x^{2/3} dx = \left[ \frac{x^{2/3+1}}{2/3+1} \right]_0^1 = \left[ \frac{x^{5/3}}{5/3} \right]_0^1 = \frac{3}{5} [x^{5/3}]_0^1 = \frac{3}{5} (1^{5/3} - 0^{5/3}) = \frac{3}{5}$.

$A_2 = \int_1^3 \sqrt{\frac{3-x}{x+1}} dx$. To evaluate this integral, we use the substitution $x = 1+2\cos(2\theta)$. Then $dx = -4\sin(2\theta) d\theta = -8\sin\theta\cos\theta d\theta$. Also, $3-x = 3-(1+2\cos(2\theta)) = 2-2\cos(2\theta) = 2(1-\cos(2\theta)) = 2(2\sin^2\theta) = 4\sin^2\theta$. And $x+1 = (1+2\cos(2\theta))+1 = 2+2\cos(2\theta) = 2(1+\cos(2\theta)) = 2(2\cos^2\theta) = 4\cos^2\theta$. So, $\sqrt{\frac{3-x}{x+1}} = \sqrt{\frac{4\sin^2\theta}{4\cos^2\theta}} = \sqrt{\tan^2\theta} = |\tan\theta|$.

Now, change the limits of integration: When $x=1$: $1 = 1+2\cos(2\theta) \implies 2\cos(2\theta) = 0 \implies \cos(2\theta) = 0$. For $x \in [1,3]$, $y \ge 0$, so we can choose $\theta \in [0, \pi/2]$. Thus, $2\theta = \pi/2 \implies \theta = \pi/4$. When $x=3$: $3 = 1+2\cos(2\theta) \implies 2\cos(2\theta) = 2 \implies \cos(2\theta) = 1$. Thus, $2\theta = 0 \implies \theta = 0$.

Since $\theta$ goes from $\pi/4$ to $0$, $\tan\theta \ge 0$, so $|\tan\theta| = \tan\theta$. $A_2 = \int_{\pi/4}^0 \tan\theta (-8\sin\theta\cos\theta) d\theta = \int_{\pi/4}^0 -8\sin^2\theta d\theta$. Reverse the limits and change the sign: $A_2 = 8 \int_0^{\pi/4} \sin^2\theta d\theta$. Using the identity $\sin^2\theta = \frac{1-\cos(2\theta)}{2}$: $A_2 = 8 \int_0^{\pi/4} \frac{1-\cos(2\theta)}{2} d\theta = 4 \int_0^{\pi/4} (1-\cos(2\theta)) d\theta$. $A_2 = 4 \left[ \theta - \frac{\sin(2\theta)}{2} \right]_0^{\pi/4}$. $A_2 = 4 \left[ \left( \frac{\pi}{4} - \frac{\sin(\pi/2)}{2} \right) - \left( 0 - \frac{\sin(0)}{2} \right) \right]$. $A_2 = 4 \left[ \frac{\pi}{4} - \frac{1}{2} \right] = \pi - 2$.

Total Area = $A_1 + A_2 = \frac{3}{5} + (\pi - 2) = \pi + \frac{3}{5} - \frac{10}{5} = \pi - \frac{7}{5}$ square units. Therefore, Option A is correct.

Since the question asks "is/are", it implies there can be multiple correct options. We have found that options A, B, and C are correct.