Question

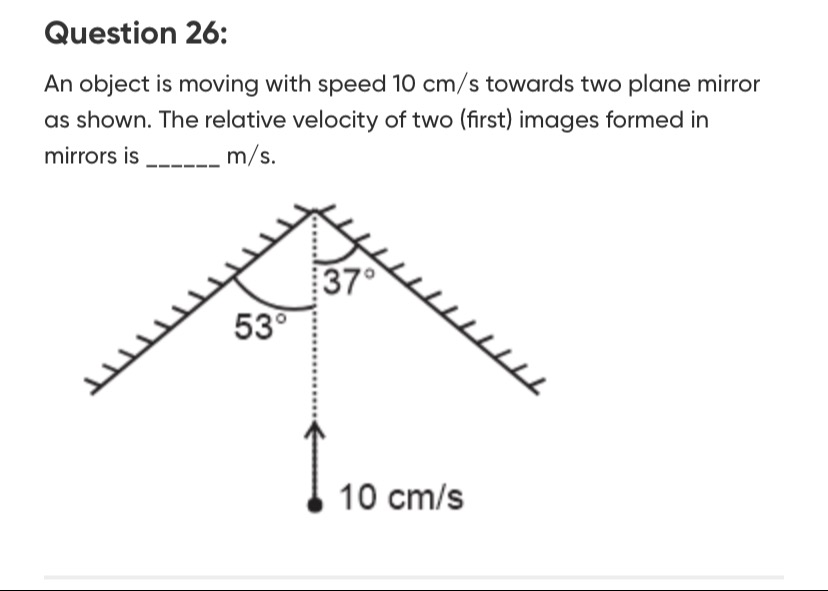
An object is moving with speed 10 cm/s towards two plane mirror as shown. The relative velocity of two (first) images formed in mirrors is ______ m/s.

Answer 1

0.20

Answer 2

To find the relative velocity of the two first images, we first determine the velocity of each image formed by the respective plane mirror. The formula for the velocity of an image ($\vec{v}_I$) formed by a stationary plane mirror, when the object velocity is $\vec{v}_O$, and the unit normal vector to the mirror pointing towards the object is $\hat{n}$, is given by:

$\vec{v}_I = \vec{v}_O - 2(\vec{v}_O \cdot \hat{n})\hat{n}$

Let's set up a coordinate system. Let the intersection point of the mirrors be the origin (0,0). The object is moving along the positive y-axis with a speed of $V = 10 \text{ cm/s}$. So, the object's velocity is $\vec{v}_O = (0, V)$.

We use the standard trigonometric values for $37^\circ$ and $53^\circ$: $\sin 37^\circ = 3/5$, $\cos 37^\circ = 4/5$, $\sin 53^\circ = 4/5$, $\cos 53^\circ = 3/5$.

1. Velocity of the image formed by the Left Mirror (Mirror 1):
The left mirror makes an angle of $53^\circ$ with the vertical (positive y-axis) towards the negative x-axis. This means the mirror itself makes an angle of $90^\circ + 53^\circ = 143^\circ$ with the positive x-axis.
The unit normal vector $\hat{n}_1$ to this mirror, pointing towards the object (which is in the upper half-plane), will make an angle of $143^\circ - 90^\circ = 53^\circ$ with the positive x-axis.
So, $\hat{n}_1 = (\cos 53^\circ, \sin 53^\circ) = (3/5, 4/5)$.

Now, calculate $\vec{v}_O \cdot \hat{n}_1$: $\vec{v}_O \cdot \hat{n}_1 = (0, V) \cdot (3/5, 4/5) = 0 \times (3/5) + V \times (4/5) = 4V/5$ The velocity of image $I_1$ is: $\vec{v}_{I1} = \vec{v}_O - 2(\vec{v}_O \cdot \hat{n}_1)\hat{n}_1$ $\vec{v}_{I1} = (0, V) - 2(4V/5)(3/5, 4/5)$ $\vec{v}_{I1} = (0, V) - (24V/25, 32V/25)$ $\vec{v}_{I1} = (-24V/25, V - 32V/25) = (-24V/25, (25V - 32V)/25)$ $\vec{v}_{I1} = (-24V/25, -7V/25)$

2. Velocity of the image formed by the Right Mirror (Mirror 2):
The right mirror makes an angle of $37^\circ$ with the vertical (positive y-axis) towards the positive x-axis. This means the mirror itself makes an angle of $90^\circ - 37^\circ = 53^\circ$ with the positive x-axis.
The unit normal vector $\hat{n}_2$ to this mirror, pointing towards the object, will make an angle of $53^\circ + 90^\circ = 143^\circ$ with the positive x-axis.
So, $\hat{n}_2 = (\cos 143^\circ, \sin 143^\circ) = (-\cos 37^\circ, \sin 37^\circ) = (-4/5, 3/5)$.

Now, calculate $\vec{v}_O \cdot \hat{n}_2$: $\vec{v}_O \cdot \hat{n}_2 = (0, V) \cdot (-4/5, 3/5) = 0 \times (-4/5) + V \times (3/5) = 3V/5$ The velocity of image $I_2$ is: $\vec{v}_{I2} = \vec{v}_O - 2(\vec{v}_O \cdot \hat{n}_2)\hat{n}_2$ $\vec{v}_{I2} = (0, V) - 2(3V/5)(-4/5, 3/5)$ $\vec{v}_{I2} = (0, V) - (-24V/25, 18V/25)$ $\vec{v}_{I2} = (24V/25, V - 18V/25) = (24V/25, (25V - 18V)/25)$ $\vec{v}_{I2} = (24V/25, 7V/25)$

3. Relative Velocity of the two images:
The relative velocity of $I_1$ with respect to $I_2$ is $\vec{v}_{rel} = \vec{v}_{I1} - \vec{v}_{I2}$. $\vec{v}_{rel} = (-24V/25, -7V/25) - (24V/25, 7V/25)$ $\vec{v}_{rel} = (-24V/25 - 24V/25, -7V/25 - 7V/25)$ $\vec{v}_{rel} = (-48V/25, -14V/25)$

The magnitude of the relative velocity is: $||\vec{v}_{rel}|| = \sqrt{(-48V/25)^2 + (-14V/25)^2}$ $||\vec{v}_{rel}|| = \sqrt{(V/25)^2 (48^2 + 14^2)}$ $||\vec{v}_{rel}|| = (V/25) \sqrt{2304 + 196}$ $||\vec{v}_{rel}|| = (V/25) \sqrt{2500}$ $||\vec{v}_{rel}|| = (V/25) \times 50$ $||\vec{v}_{rel}|| = 2V$

Given $V = 10 \text{ cm/s}$. $||\vec{v}_{rel}|| = 2 \times 10 \text{ cm/s} = 20 \text{ cm/s}$ Convert to m/s: $20 \text{ cm/s} = 20 \times 10^{-2} \text{ m/s} = 0.20 \text{ m/s}$