Question

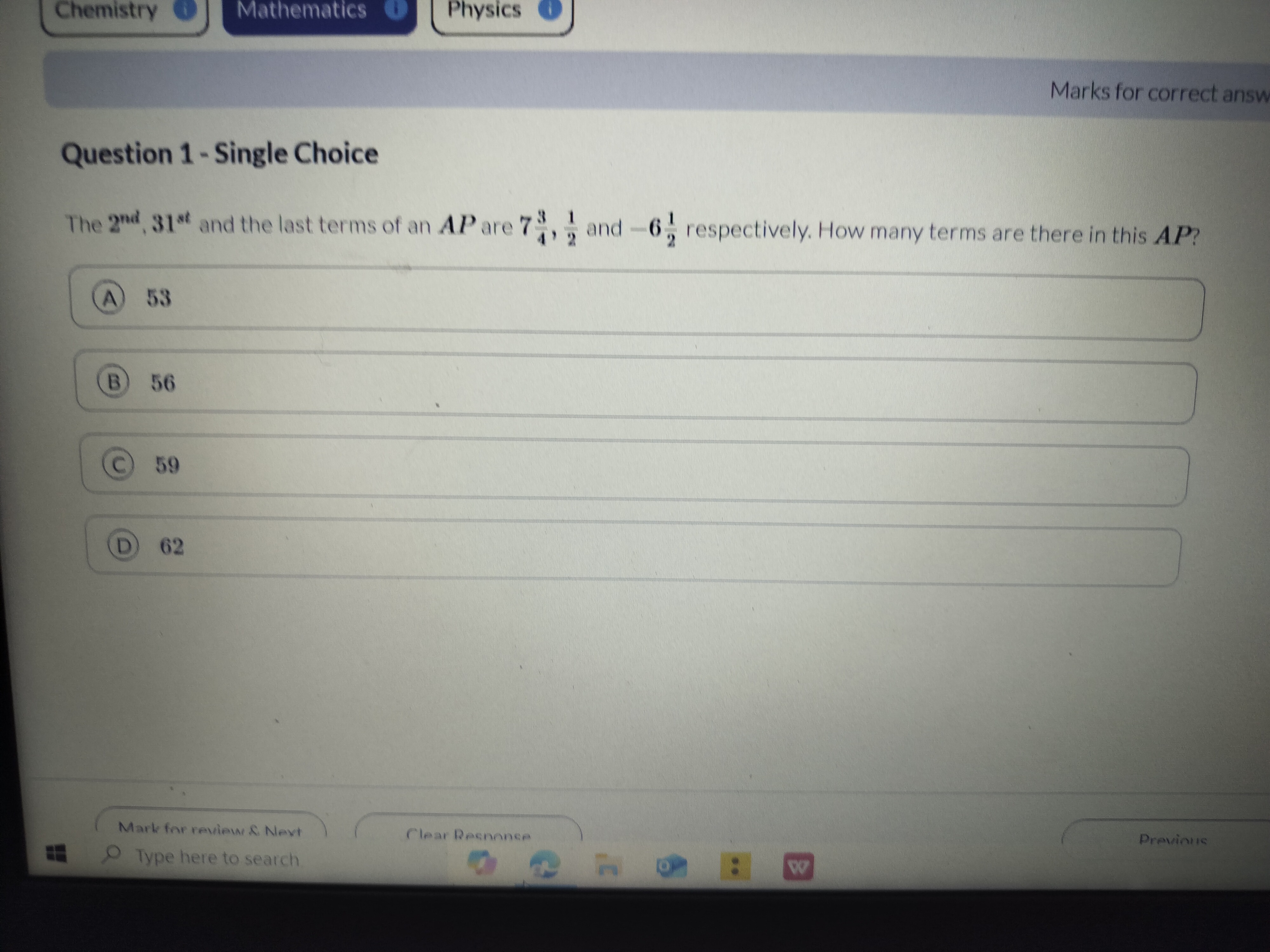
The 2nd, 31st and the last terms of an $AP$ are $7\frac{3}{4}$, $\frac{1}{2}$ and $-6\frac{1}{2}$ respectively. How many terms are there in this $AP$?

• A. 53
• B. 56
• C. 59
• D. 62

Answer 1

Answer: (C)

59

Answer 2

To find the number of terms in the Arithmetic Progression (AP), we can use the information given about the 2nd, 31st, and last terms.

Let $a$ be the first term and $d$ be the common difference. The $n$-th term of an AP is given by:

$a_n = a + (n-1)d$

We have:

1. $a_2 = a + d = 7\frac{3}{4} = \frac{31}{4}$
2. $a_{31} = a + 30d = \frac{1}{2}$
3. $a_N = a + (N-1)d = -6\frac{1}{2} = -\frac{13}{2}$, where $N$ is the total number of terms.

Subtracting equation (1) from equation (2):

$29d = \frac{1}{2} - \frac{31}{4} = \frac{2}{4} - \frac{31}{4} = -\frac{29}{4}$

So, $d = -\frac{1}{4}$.

Substituting $d$ into equation (1):

$a - \frac{1}{4} = \frac{31}{4}$

$a = \frac{32}{4} = 8$

Now, using equation (3) to find $N$:

$8 + (N-1)\left(-\frac{1}{4}\right) = -\frac{13}{2}$

Multiplying by 4 to eliminate fractions:

$32 - (N-1) = -26$

$32 - N + 1 = -26$

$33 - N = -26$

$N = 33 + 26 = 59$

Therefore, there are 59 terms in the AP.