Question

The sum to n term of the series 1(1!)+2(2!)+3(3!) + ....

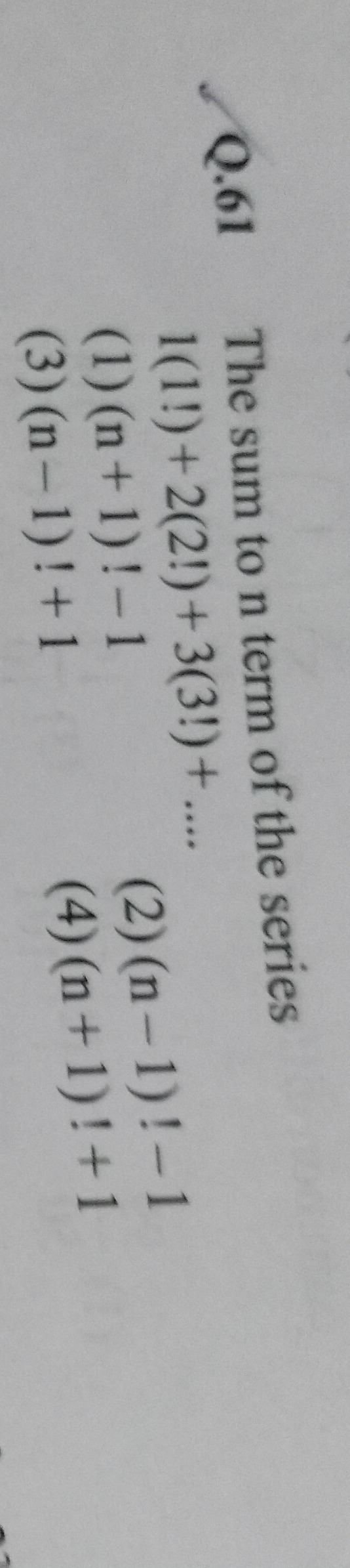
• A. (n+1)!-1
• B. (n-1)! - 1
• C. (n-1)! +1
• D. (n+1)! +1

Answer 1

Answer: (A)

(n+1)! - 1

Answer 2

The n-th term of the series is $T_n = n(n!)$. We can rewrite $T_n$ as: $T_n = (n+1-1)n!$ $T_n = (n+1)n! - 1 \cdot n!$ $T_n = (n+1)! - n!$

The sum of the first n terms, $S_n$, is given by: $S_n = \sum_{k=1}^{n} T_k = \sum_{k=1}^{n} ((k+1)! - k!)$

This is a telescoping series. Expanding the sum: $S_n = (2! - 1!) + (3! - 2!) + (4! - 3!) + \dots + ((n+1)! - n!)$

All intermediate terms cancel out, leaving: $S_n = (n+1)! - 1!$ Since $1! = 1$, $S_n = (n+1)! - 1$