Question

m₁ and m₂ are connected with a light inextensible string with m₁ lying on smooth table and m₂ hanging as shown in figure. m₁ is also connected to a light spring which is initially unstretched and the system is released from rest

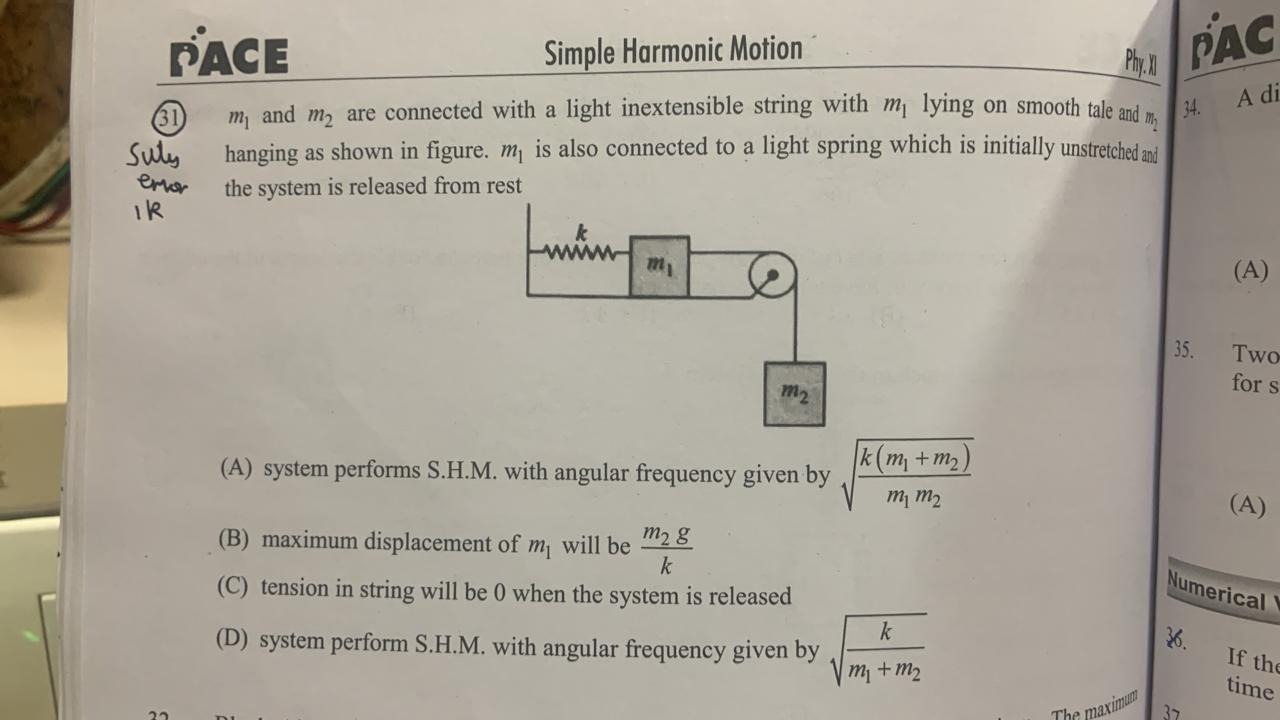
• A. system performs S.H.M. with angular frequency given by $\displaystyle \sqrt{\frac{k\,(m_1 + m_2)}{m_1\,m_2}}$
• B. maximum displacement of $m_1$ will be $\dfrac{m_2\,g}{k}$
• C. tension in string will be 0 when the system is released
• D. system perform S.H.M. with angular frequency given by $\displaystyle \sqrt{\frac{k}{m_1 + m_2}}$

Answer 1

Answer: (B), (C), (D)

maximum displacement of $m_1$ will be $\dfrac{m_2\,g}{k}$; tension in string will be 0 when the system is released; system perform S.H.M. with angular frequency given by $\displaystyle \sqrt{\frac{k}{m_1 + m_2}}$

Answer 2

1. Equations of motion and equilibrium

• Let the extension of the spring (and displacement of both masses) be $x$ downward/rightward.
• For $m_1$ on the table: $$m_1\,\ddot x = T - k\,x.$$
• For $m_2$ hanging: $$m_2\,\ddot x = m_2\,g - T.$$
• Adding gives: $$(m_1 + m_2)\,\ddot x + k\,x - m_2\,g = 0.$$

2. Equilibrium extension $x_0$

• At equilibrium $\ddot x=0$, so $k\,x_0 = m_2\,g$.
• Thus $x_0 = \dfrac{m_2\,g}{k}$.

3. Simple Harmonic Motion about equilibrium

• Define $y = x - x_0$. Substituting yields: $$(m_1 + m_2)\,\ddot y + k\,y = 0 \quad\Longrightarrow\quad \omega = \sqrt{\frac{k}{m_1 + m_2}}.$$

4. Initial conditions and amplitude

• Initially $x(0)=0$ (spring unstretched), so $y(0) = -x_0$.
• The amplitude of oscillation is $|y(0)| = x_0 = \dfrac{m_2\,g}{k}$.
• Hence maximum displacement of $m_1$ from the equilibrium position is $x_0$.

5. Tension at release

• At $t=0$, spring force $=0$, so string is slack ⇒ tension $T=0$.