Question

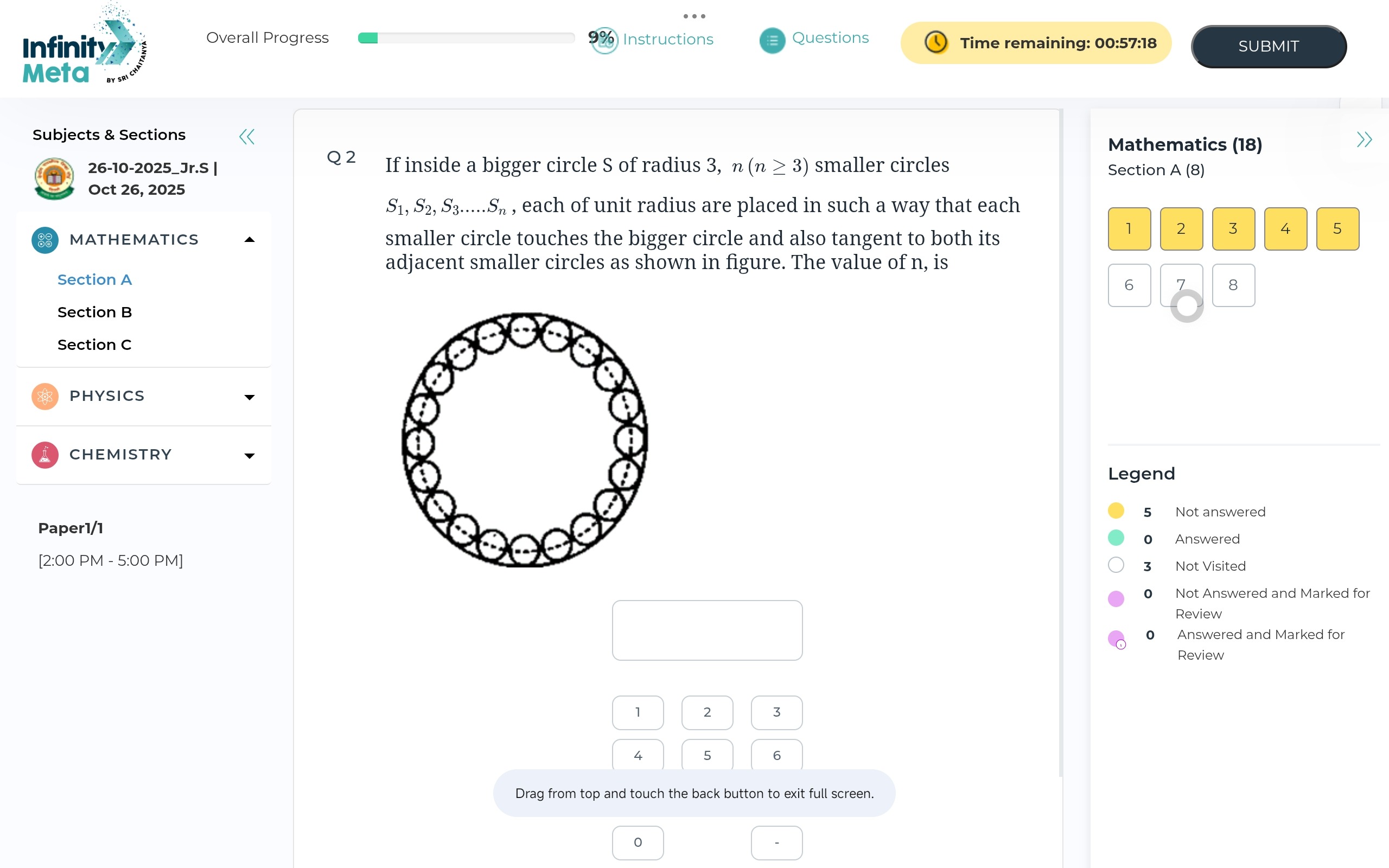
If inside a bigger circle S of radius 3, $n (n \geq 3)$ smaller circles $S_1, S_2, S_3..... S_n$, each of unit radius are placed in such a way that each smaller circle touches the bigger circle and also tangent to both its adjacent smaller circles as shown in figure. The value of n, is

• A. 1
• B. 2
• C. 3
• D. 4
• E. 5
• F. 6

Answer 1

Answer: (F)

6

Answer 2

Let $R$ be the radius of the bigger circle and $r$ be the radius of the smaller circles. We are given $R=3$ and $r=1$. The distance from the center of the bigger circle to the center of each smaller circle is $R-r = 3-1=2$. The distance between the centers of two adjacent smaller circles is $r+r = 1+1=2$. The centers of the smaller circles form a regular $n$-gon with side length 2, inscribed in a circle of radius 2. For a regular $n$-gon inscribed in a circle of radius $a$ with side length $s$, the relation is $s = 2a \sin(\frac{\pi}{n})$. Substituting the values, $2 = 2(2) \sin(\frac{\pi}{n})$, which simplifies to $\sin(\frac{\pi}{n}) = \frac{1}{2}$. Since $n \ge 3$, the only solution is $\frac{\pi}{n} = \frac{\pi}{6}$, which gives $n=6$.