Question

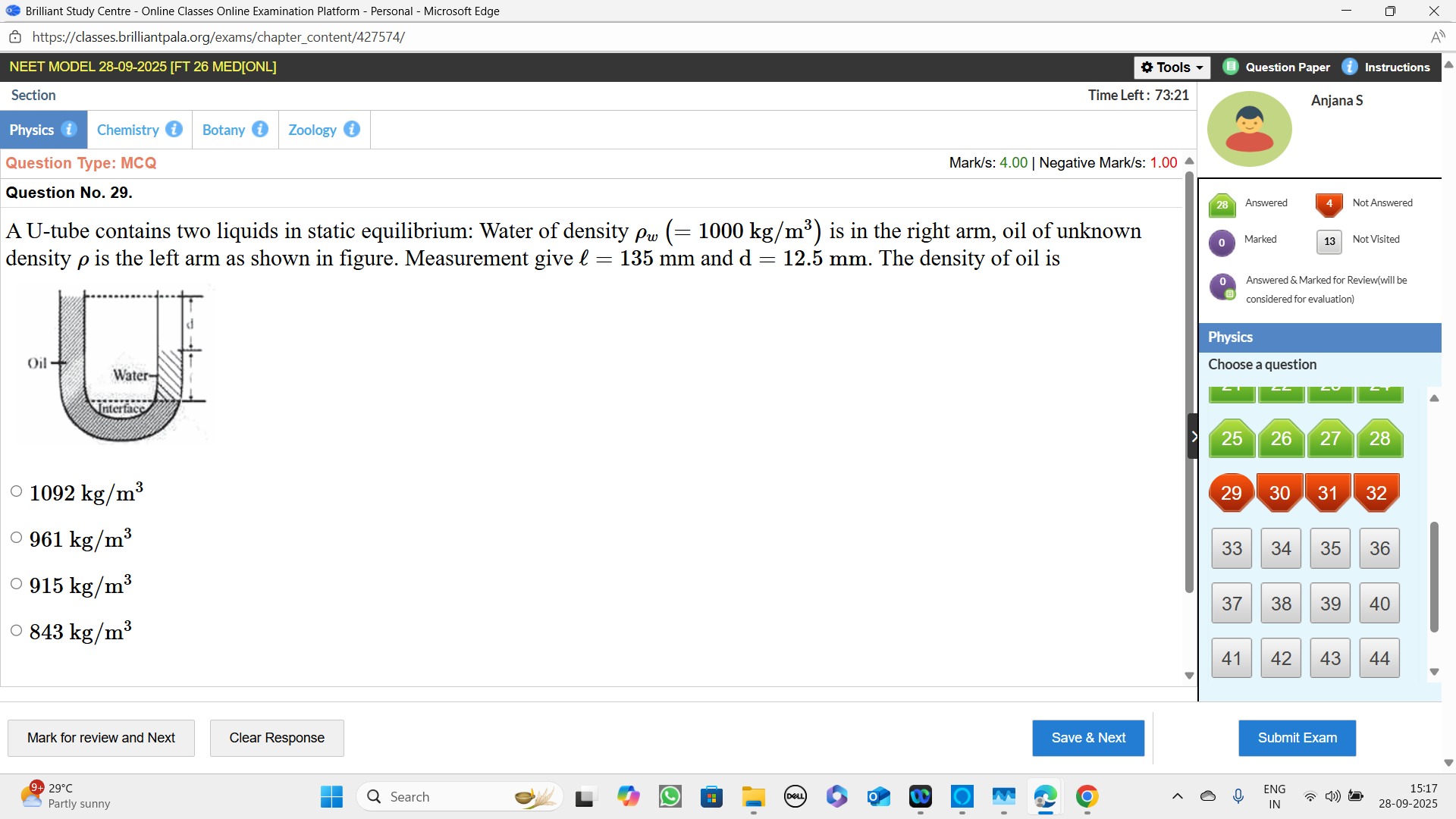
A U-tube contains two liquids in static equilibrium: Water of density $\rho_w$ (= 1000 kg/m³) is in the right arm, oil of unknown density $\rho$ is the left arm as shown in figure. Measurement give $l$ = 135 mm and d = 12.5 mm. The density of oil is

• A. 1092 kg/m³
• B. 961 kg/m³
• C. 915 kg/m³
• D. 843 kg/m³

Answer 1

Answer: (C)

915 kg/m³

Answer 2

The principle of hydrostatic equilibrium states that the pressure at the same horizontal level in a continuous fluid is equal. Considering the horizontal level at the interface between the oil and water: Pressure in the right arm (water): $P_{right} = P_{atm} + \rho_w g l$ Pressure in the left arm (oil): $P_{left} = P_{atm} + \rho g (l+d)$ Equating the pressures: $P_{atm} + \rho_w g l = P_{atm} + \rho g (l+d)$ $\rho_w l = \rho (l+d)$ Solving for $\rho$: $\rho = \rho_w \frac{l}{l+d}$ Substituting the given values: $\rho = 1000 \text{ kg/m³} \times \frac{135 \text{ mm}}{135 \text{ mm} + 12.5 \text{ mm}}$ $\rho = 1000 \text{ kg/m³} \times \frac{135}{147.5}$ $\rho = 1000 \times \frac{1350}{1475} = 1000 \times \frac{54}{59} \approx 915.254 \text{ kg/m³}$ The closest option is 915 kg/m³.