Question
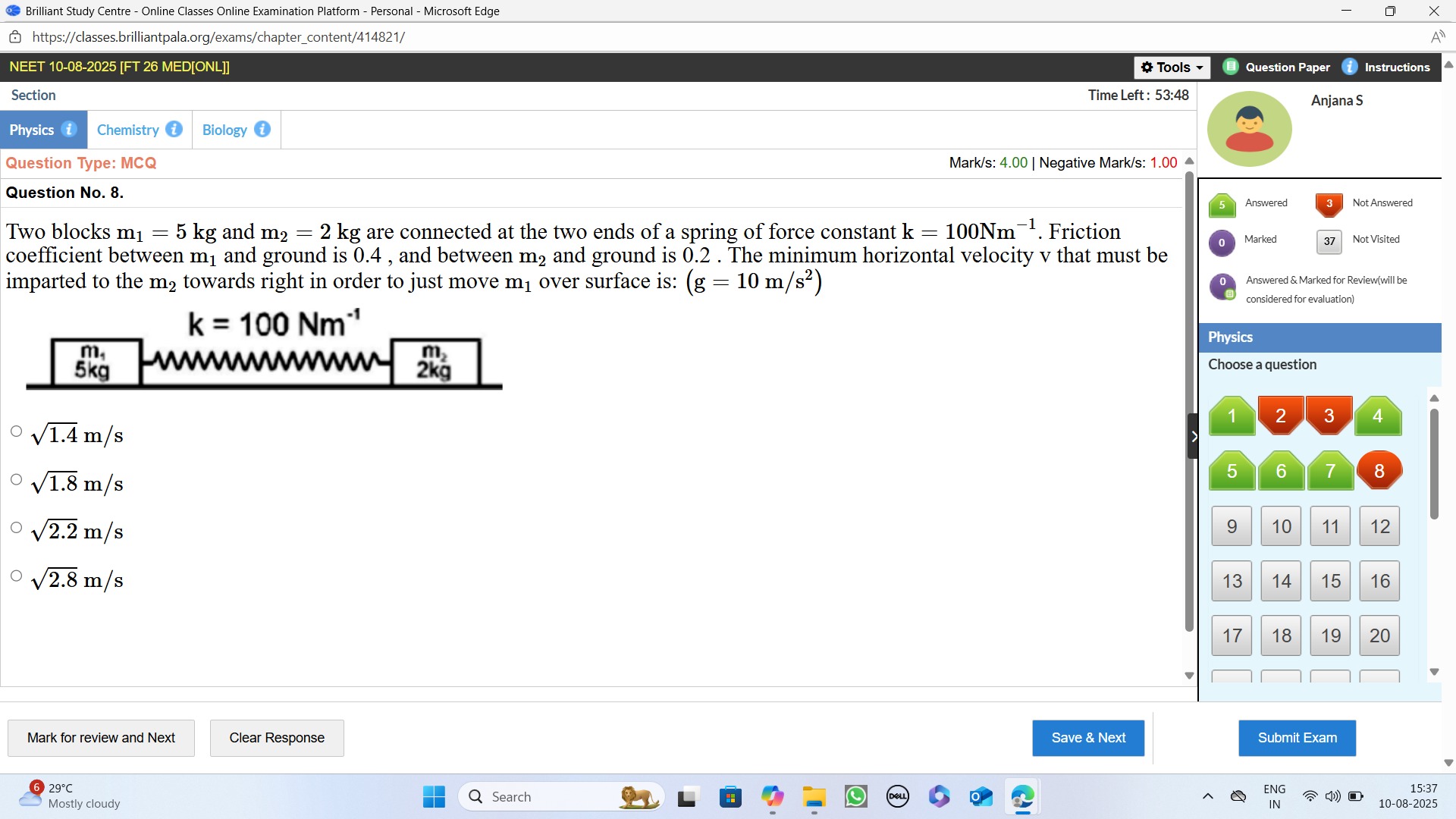
Question: Two blocks $m_1$ = 5 kg and $m_2$ = 2 kg are connected at the two ends of a spring of force constant...
Two blocks m1 = 5 kg and m2 = 2 kg are connected at the two ends of a spring of force constant k = 100Nm−1. Friction coefficient between m1 and ground is 0.4, and between m2 and ground is 0.2 . The minimum horizontal velocity v that must be imparted to the m2 towards right in order to just move m1 over surface is: (g = 10 m/s2)
1.4 m/s
1.8 m/s
2.2 m/s
2.8 m/s
2.8 m/s
Solution
To solve this problem, we need to determine the minimum initial velocity v imparted to block m_2 such that block m_1 just begins to move.
Step 1: Determine the critical spring compression x_0 for m_1 to just move.
For m_1 to just move, the force exerted by the spring (F_s) on m_1 must be equal to the maximum static friction force (f_{s1,max}) on m_1.
The maximum static friction force on m_1 is given by:
fs1,max=μ1N1=μ1m1g
The spring force when compressed by x_0 is:
Fs=kx0
Equating these two forces for m_1 to just move:
kx0=μ1m1g
x0=kμ1m1g
Given values: m1=5 kg μ1=0.4 g=10 m/s2 k=100 Nm−1
Substitute the values: x0=1000.4×5×10=10020=0.2 m
Step 2: Apply the Work-Energy Theorem to the system of m_2 and the spring.
For the minimum initial velocity v for m_2, we assume that m_2 comes to a momentary stop (its velocity becomes zero) exactly when the spring is compressed by x_0. This ensures that all the initial kinetic energy of m_2 is used to compress the spring and overcome the friction on m_2.
Consider the initial state (when m_2 is given velocity v, spring is at natural length) and the final state (when m_2 momentarily stops and the spring is compressed by x_0).
Initial Kinetic Energy of m_2: KEi=21m2v2
Final Kinetic Energy of m_2: KEf=0 (since m_2 momentarily stops)
Initial Spring Potential Energy: PEi=0 (spring is at natural length) Final Spring Potential Energy: PEf=21kx02
Work done by friction on m_2 (Wf2): Friction force on m_2 is f2=μ2N2=μ2m2g. This force opposes the displacement x_0.
Wf2=−f2x0=−μ2m2gx0
According to the Work-Energy Theorem: ΔKE+ΔPE=Wf2 (KEf−KEi)+(PEf−PEi)=Wf2 (0−21m2v2)+(21kx02−0)=−μ2m2gx0 −21m2v2+21kx02=−μ2m2gx0
Rearrange the equation to solve for v2: 21m2v2=21kx02+μ2m2gx0 Multiply by 2: m2v2=kx02+2μ2m2gx0 v2=m2kx02+2μ2gx0
Given values: m2=2 kg μ2=0.2 g=10 m/s2 k=100 Nm−1 x0=0.2 m
Substitute these values into the equation for v2: v2=2100×(0.2)2+2×0.2×10×0.2 v2=2100×0.04+0.8 v2=24+0.8 v2=2+0.8 v2=2.8
Therefore, the minimum horizontal velocity v is:
v=2.8 m/s
