Question
Question: $\displaystyle = \lim_{x\to3} \left[ \frac{\sqrt{2x+6}}{x} \right]$...
=x→3lim[x2x+6]
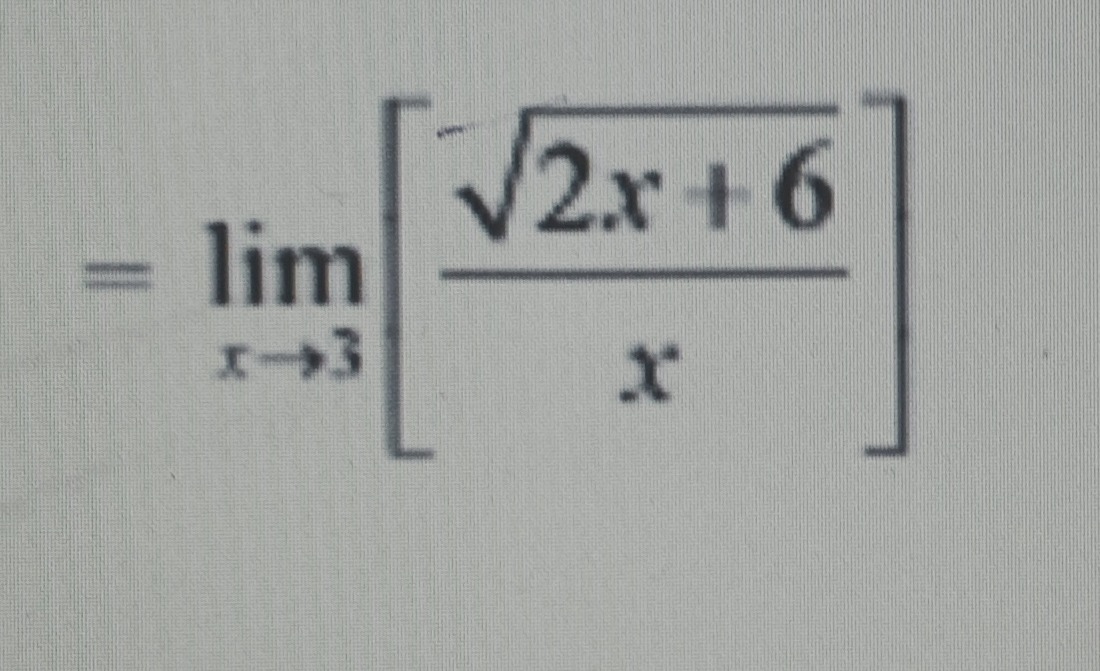
Answer
323
Explanation
Solution
We want to evaluate the limit:
L=x→3lim[x2x+6]
The function is f(x)=x2x+6.
We can try direct substitution of x=3 into the function.
Numerator: 2(3)+6=6+6=12
Denominator: 3
Since the denominator is non-zero at x=3 and the numerator is defined (the expression inside the square root is positive), the function is continuous at x=3.
Therefore, the limit can be found by direct substitution:
L=32(3)+6=36+6=312
Now, we simplify the expression:
12=4×3=4×3=23
So, the limit is:
L=323
The limit is evaluated by direct substitution of x=3 into the expression, as the function is continuous at x=3. Substituting x=3 gives 32(3)+6=312. Simplifying 12 to 23 gives the final result 323.
