Question

$$L = \lim_{x \to 0} \frac{\int_{0}^{\sin^2 x} ln(1+t^3) dt}{\int_{0}^{x} (e^t-1-t)(\tan t - t)(1-\cos t) dt}$$

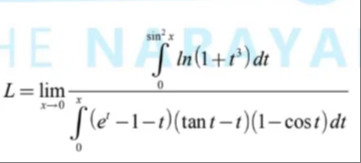
Answer 1

24

Answer 2

To solve this limit, we use small-angle approximations and Taylor series expansions.

Numerator Analysis:

For small $t$, $\ln(1+t^3) \approx t^3$. Also, for small $x$, $\sin^2 x \approx x^2$. Therefore,

$$\int_{0}^{\sin^2 x} \ln(1+t^3) \, dt \approx \int_0^{x^2} t^3 \, dt = \frac{t^4}{4} \Big|_0^{x^2} = \frac{(x^2)^4}{4} = \frac{x^8}{4}.$$

Denominator Analysis:

For small $t$, we have the following approximations:

$$e^t - 1 - t \approx \frac{t^2}{2}, \quad \tan t - t \approx \frac{t^3}{3}, \quad 1-\cos t \approx \frac{t^2}{2}.$$

Therefore,

$$(e^t-1-t)(\tan t-t)(1-\cos t) \approx \left(\frac{t^2}{2}\right) \left(\frac{t^3}{3}\right) \left(\frac{t^2}{2}\right) = \frac{t^7}{12}.$$

Thus,

$$\int_{0}^{x} (e^t-1-t)(\tan t-t)(1-\cos t) \, dt \approx \int_0^x \frac{t^7}{12} \, dt = \frac{t^8}{12 \cdot 8} \Big|_0^x = \frac{x^8}{96}.$$

Taking the Limit:

$$L = \lim_{x \to 0} \frac{\frac{x^8}{4}}{\frac{x^8}{96}} = \frac{\frac{1}{4}}{\frac{1}{96}} = \frac{96}{4} = 24.$$

Therefore, the limit is 24.