Question

If $y = \log \tan \left( \frac{x}{2} \right) + \sin^{-1} (\cos x)$, then $\frac{dy}{dx} =$

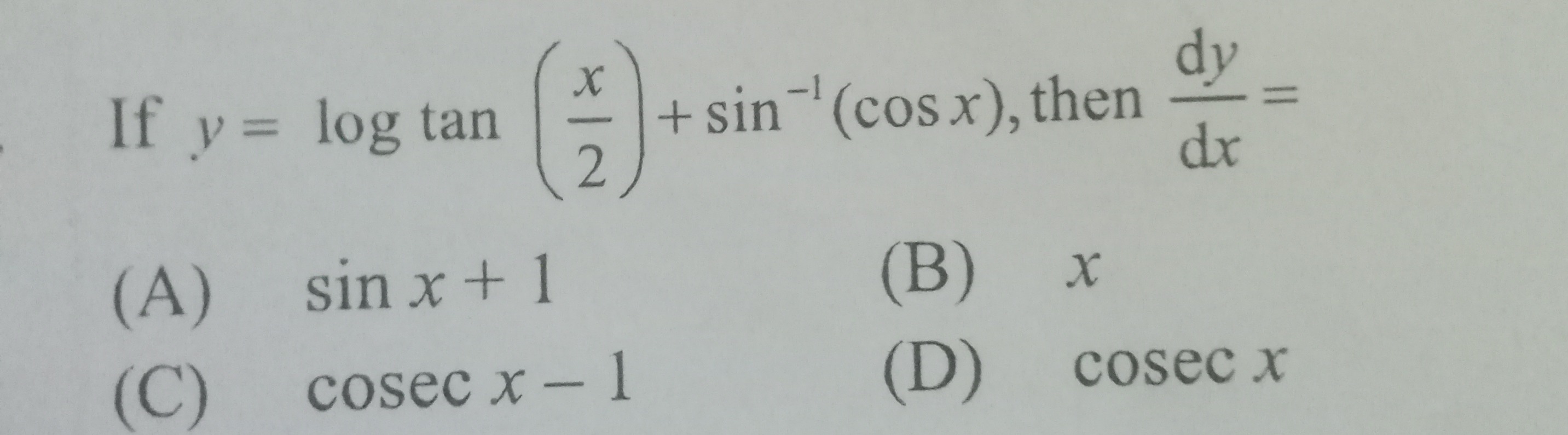
• A. $\sin x + 1$
• B. $x$
• C. $\csc x - 1$
• D. $\csc x$

Answer 1

Answer: (C)

$\csc x - 1$

Answer 2

Step 1:
Differentiate $\ln\tan\frac{x}{2}$:

$$\frac{d}{dx}\bigl[\ln\tan\frac{x}{2}\bigr] = \frac{1}{\tan\frac{x}{2}}\cdot\sec^2\frac{x}{2}\cdot\frac12 = \frac{\sec^2\frac{x}{2}}{2\tan\frac{x}{2}} = \frac{1}{2\sin\frac{x}{2}\cos\frac{x}{2}} = \frac{1}{\sin x} = \csc x.$$

Step 2:
Differentiate $\sin^{-1}(\cos x)$: let $u=\cos x$. Then

$$\frac{d}{dx}[\sin^{-1}(u)] = \frac{u'}{\sqrt{1-u^2}} = \frac{-\sin x}{\sqrt{1-\cos^2 x}} = \frac{-\sin x}{|\sin x|}.$$

For $0<x<\pi$, $\sin x>0$, so this becomes $-1$.

Combine:

$$\frac{dy}{dx} = \csc x + (-1) = \csc x - 1.$$