Question
Question: If $I_1 = \int_0^1 (1-x^{50})^{100} dx$, $I_2 = \int_0^1 (1-x^{50})^{101} dx$ and $I_2 = \alpha I_1$...
If I1=∫01(1−x50)100dx, I2=∫01(1−x50)101dx and I2=αI1, then α equal
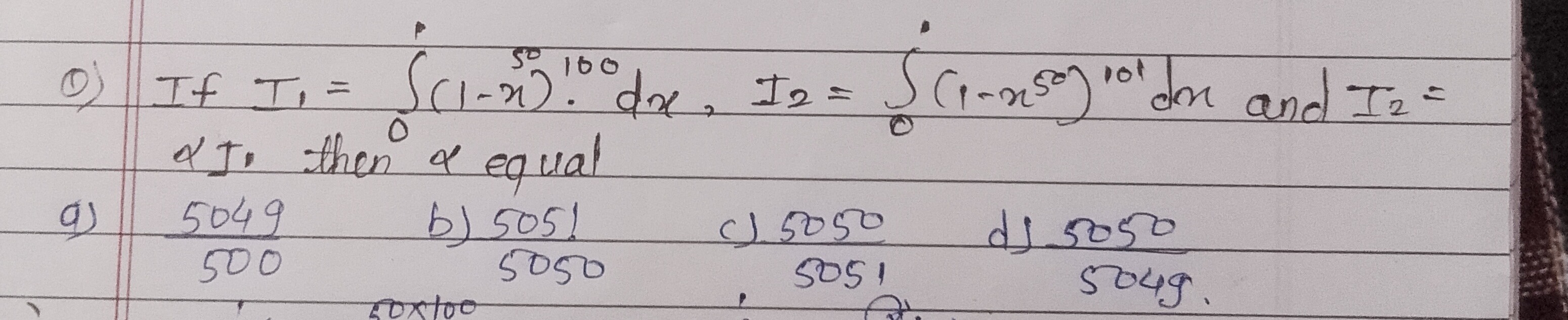
5005049
50505051
50515050
50495050
c
Solution
To find the value of α such that I2=αI1, we need to establish a relationship between I1 and I2. Let's define a general integral I(n)=∫01(1−x50)ndx. So, I1=I(100) and I2=I(101).
We will use integration by parts for I(n). Let u=(1−x50)n and dv=dx. Then, du=n(1−x50)n−1(−50x49)dx=−50nx49(1−x50)n−1dx. And, v=x.
Applying the integration by parts formula ∫udv=uv−∫vdu: I(n)=[x(1−x50)n]01−∫01x(−50nx49(1−x50)n−1)dx
Evaluate the definite part: [x(1−x50)n]01=1⋅(1−150)n−0⋅(1−050)n=1⋅0n−0⋅1n=0−0=0 (since n≥1).
So, the integral becomes: I(n)=0−∫01(−50nx50(1−x50)n−1)dx I(n)=50n∫01x50(1−x50)n−1dx
Now, we need to express x50 in terms of (1−x50) to relate it back to I(n) or I(n−1). We can write x50=1−(1−x50). Substitute this into the integral: I(n)=50n∫01(1−(1−x50))(1−x50)n−1dx I(n)=50n∫01[(1−x50)n−1−(1−x50)n]dx I(n)=50n[∫01(1−x50)n−1dx−∫01(1−x50)ndx]
Recognize the terms as I(n−1) and I(n): I(n)=50n[I(n−1)−I(n)]
Now, we solve for I(n): I(n)=50nI(n−1)−50nI(n) I(n)+50nI(n)=50nI(n−1) I(n)(1+50n)=50nI(n−1) I(n)=50n+150nI(n−1)
This is a reduction formula. We need to find α such that I2=αI1. Here, I2=I(101) and I1=I(100). Using the reduction formula with n=101: I(101)=50×101+150×101I(101−1) I2=5050+15050I(100) I2=50515050I1
Comparing this with I2=αI1, we find: α=50515050
