Question

If $i^2 = -1$, then for a complex number $Z$ the minimum value of $|Z|+|Z-3|+|Z+i|+|Z-3-2i|$ occurs at

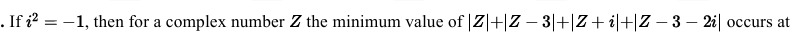
• A. 1
• B. 2
• C. 3
• D. 4

Answer 1

Answer: (A)

1

Answer 2

Let the four points be $P_1(0,0)$, $P_2(3,0)$, $P_3(0,-1)$, $P_4(3,2)$. The sum of distances $|Z-P_1| + |Z-P_2| + |Z-P_3| + |Z-P_4|$ is minimized at the geometric median. For four points, if they form a convex quadrilateral, the geometric median is the intersection of its diagonals.

The convex hull of these points forms the quadrilateral $P_3P_1P_2P_4$ (i.e., $CABD$). The diagonals of this convex quadrilateral are $P_1P_2$ and $P_3P_4$.

1. Line $P_1P_2$: connecting $(0,0)$ and $(3,0)$ is $y=0$.
2. Line $P_3P_4$: connecting $(0,-1)$ and $(3,2)$ is $y - (-1) = \frac{2-(-1)}{3-0}(x-0) \implies y+1 = x \implies y=x-1$.

Equating the $y$-values to find the intersection:

$0 = x-1 \implies x=1$.

The intersection point is $(1,0)$, which corresponds to the complex number $Z=1+0i=1$. This point lies within the convex quadrilateral defined by the points.