Question

If $\alpha, \beta, \gamma \in R$, PT

(i) $Sin\alpha + Sin\beta + Sin\gamma - Sin(\alpha + \beta + \gamma) = 4 Sin(\frac{\alpha + \beta}{2})Cos(\frac{\beta + \gamma}{2}) \times Cos(\frac{\alpha + \gamma}{2})$

(ii) $Cos\alpha + Cos\beta + Cos\gamma - Cos(\alpha + \beta + \gamma) = 4 Cos(\frac{\alpha + \beta}{2})Cos(\frac{\beta + \gamma}{2})Cos(\frac{\alpha + \gamma}{2})$

Answer 1

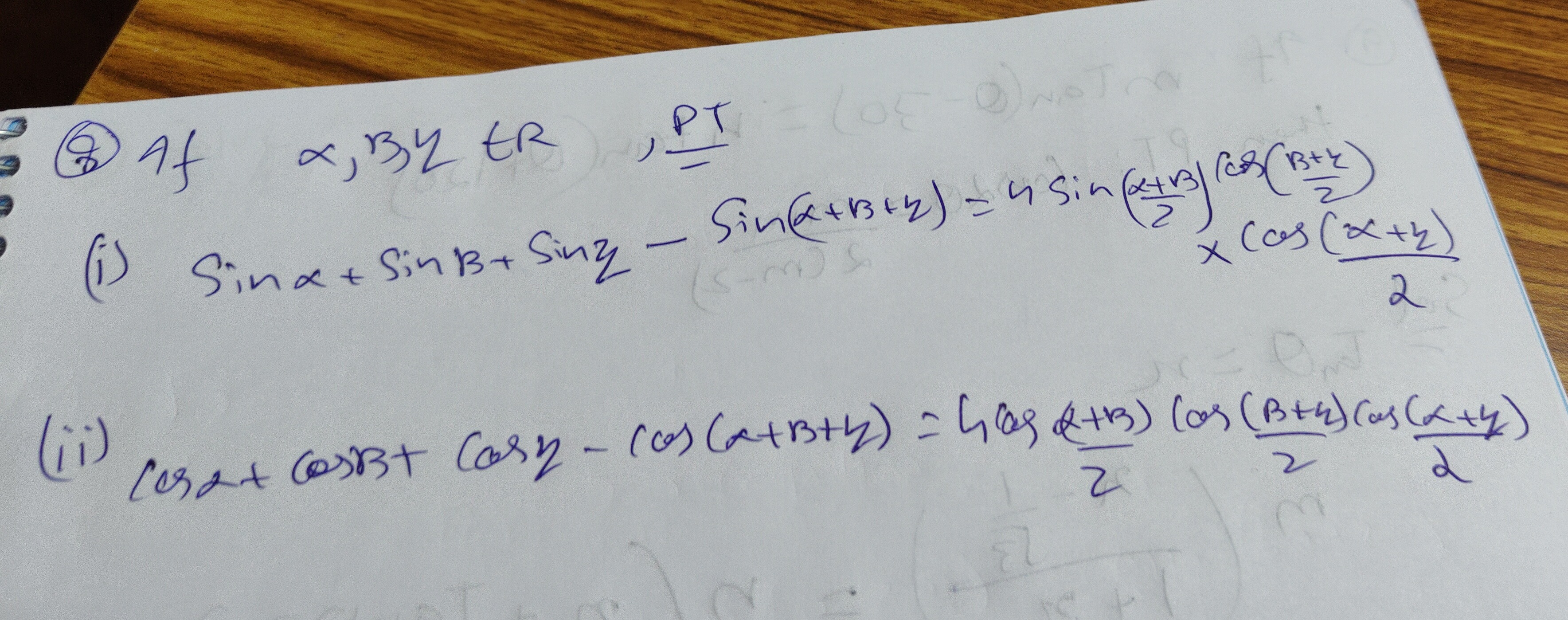
The identities as stated in the question are incorrect. The correct identities are:

(i) $Sin\alpha + Sin\beta + Sin\gamma - Sin(\alpha + \beta + \gamma) = 4 Sin(\frac{\alpha + \beta}{2})Sin(\frac{\beta + \gamma}{2})Sin(\frac{\alpha + \gamma}{2})$

(ii) $Cos\alpha + Cos\beta + Cos\gamma + Cos(\alpha + \beta + \gamma) = 4 Cos(\frac{\alpha + \beta}{2})Cos(\frac{\beta + \gamma}{2})Cos(\frac{\alpha + \gamma}{2})$

Answer 2

The given identities are incorrect. The correct identities are:

(i) $Sin\alpha + Sin\beta + Sin\gamma - Sin(\alpha + \beta + \gamma) = 4 Sin(\frac{\alpha + \beta}{2})Sin(\frac{\beta + \gamma}{2})Sin(\frac{\alpha + \gamma}{2})$

(ii) $Cos\alpha + Cos\beta + Cos\gamma + Cos(\alpha + \beta + \gamma) = 4 Cos(\frac{\alpha + \beta}{2})Cos(\frac{\beta + \gamma}{2})Cos(\frac{\alpha + \gamma}{2})$

Proof for (i):

Starting with the left-hand side (LHS):

$LHS = Sin\alpha + Sin\beta + Sin\gamma - Sin(\alpha + \beta + \gamma)$

Using the sum-to-product formula, $SinX + SinY = 2Sin(\frac{X+Y}{2})Cos(\frac{X-Y}{2})$:

$Sin\alpha + Sin\beta = 2Sin(\frac{\alpha + \beta}{2})Cos(\frac{\alpha - \beta}{2})$

Using the difference-to-product formula, $SinX - SinY = 2Cos(\frac{X+Y}{2})Sin(\frac{X-Y}{2})$:

$Sin\gamma - Sin(\alpha + \beta + \gamma) = 2Cos(\frac{\gamma + \alpha + \beta + \gamma}{2})Sin(\frac{\gamma - (\alpha + \beta + \gamma)}{2})$ $= 2Cos(\frac{\alpha + \beta + 2\gamma}{2})Sin(\frac{-\alpha - \beta}{2})$ $= -2Cos(\frac{\alpha + \beta + 2\gamma}{2})Sin(\frac{\alpha + \beta}{2})$

Combining these:

$LHS = 2Sin(\frac{\alpha + \beta}{2})Cos(\frac{\alpha - \beta}{2}) - 2Cos(\frac{\alpha + \beta + 2\gamma}{2})Sin(\frac{\alpha + \beta}{2})$ $= 2Sin(\frac{\alpha + \beta}{2})[Cos(\frac{\alpha - \beta}{2}) - Cos(\frac{\alpha + \beta + 2\gamma}{2})]$

Using the difference of cosines formula, $CosX - CosY = -2Sin(\frac{X+Y}{2})Sin(\frac{X-Y}{2})$:

$Cos(\frac{\alpha - \beta}{2}) - Cos(\frac{\alpha + \beta + 2\gamma}{2}) = -2Sin(\frac{\alpha - \beta + \alpha + \beta + 2\gamma}{4})Sin(\frac{\alpha - \beta - \alpha - \beta - 2\gamma}{4})$ $= -2Sin(\frac{2\alpha + 2\gamma}{4})Sin(\frac{-2\beta - 2\gamma}{4})$ $= 2Sin(\frac{\alpha + \gamma}{2})Sin(\frac{\beta + \gamma}{2})$

Substituting back:

$LHS = 2Sin(\frac{\alpha + \beta}{2})[2Sin(\frac{\alpha + \gamma}{2})Sin(\frac{\beta + \gamma}{2})]$ $LHS = 4Sin(\frac{\alpha + \beta}{2})Sin(\frac{\beta + \gamma}{2})Sin(\frac{\alpha + \gamma}{2})$

Proof for (ii):

Starting with the right-hand side (RHS):

$RHS = 4 Cos(\frac{\alpha + \beta}{2})Cos(\frac{\beta + \gamma}{2})Cos(\frac{\alpha + \gamma}{2})$

Using the product-to-sum formula, $2CosA CosB = Cos(A+B) + Cos(A-B)$:

$RHS = 2Cos(\frac{\alpha + \beta}{2})[Cos(\frac{\beta + \gamma + \alpha + \gamma}{2}) + Cos(\frac{\beta + \gamma - \alpha - \gamma}{2})]$ $= 2Cos(\frac{\alpha + \beta}{2})[Cos(\frac{\alpha + \beta + 2\gamma}{2}) + Cos(\frac{\beta - \alpha}{2})]$ $= 2Cos(\frac{\alpha + \beta}{2})[Cos(\frac{\alpha + \beta + 2\gamma}{2}) + Cos(\frac{\alpha - \beta}{2})]$

Expanding further:

$RHS = Cos(\frac{\alpha + \beta + \alpha + \beta + 2\gamma}{2}) + Cos(\frac{\alpha + \beta - \alpha - \beta - 2\gamma}{2}) + Cos(\frac{\alpha + \beta + \alpha - \beta}{2}) + Cos(\frac{\alpha + \beta - \alpha + \beta}{2})$ $= Cos(\alpha + \beta + \gamma) + Cos(-\gamma) + Cos(\alpha) + Cos(\beta)$ $= Cos(\alpha + \beta + \gamma) + Cos(\gamma) + Cos(\alpha) + Cos(\beta)$ $= Cos\alpha + Cos\beta + Cos\gamma + Cos(\alpha + \beta + \gamma)$

Thus, the corrected identities are proven.