Question

$$f(x) = \begin{cases} x.\frac{\ln(1+x)+\ln(1-x)}{\sec x - \cos x}, & x \in (-1,0) \\ (k^2 - 3k - 1)\sin x + x^2, & x \in [0, \infty) \end{cases}$$

Let $k_1$ & $k_2$ be two values of k for which is differentiable at x = 0, then the value of $(k_1^2 + k_2^2 - 3)$ is equal to

Answer 1

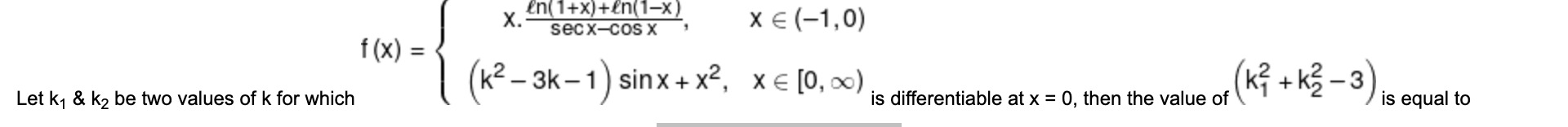
6

Answer 2

The function is given by:

$$f(x) = \begin{cases} x.\frac{\ln(1+x)+\ln(1-x)}{\sec x - \cos x}, & x \in (-1,0) \\ (k^2 - 3k - 1)\sin x + x^2, & x \in [0, \infty) \end{cases}$$

For $f(x)$ to be differentiable at $x=0$, it must first be continuous at $x=0$.

Step 1: Check for continuity at $x=0$.

For continuity at $x=0$, we need $\lim_{x \to 0^-} f(x) = \lim_{x \to 0^+} f(x) = f(0)$.

$f(0) = (k^2 - 3k - 1)\sin(0) + 0^2 = 0$.

$\lim_{x \to 0^+} f(x) = \lim_{x \to 0^+} [(k^2 - 3k - 1)\sin x + x^2] = (k^2 - 3k - 1)\sin(0) + 0^2 = 0$.

$\lim_{x \to 0^-} f(x) = \lim_{x \to 0^-} x.\frac{\ln(1+x)+\ln(1-x)}{\sec x - \cos x}$.

Using $\ln(1+x)+\ln(1-x) = \ln((1+x)(1-x)) = \ln(1-x^2)$ and $\sec x - \cos x = \frac{1}{\cos x} - \cos x = \frac{1-\cos^2 x}{\cos x} = \frac{\sin^2 x}{\cos x}$.

The expression becomes $\lim_{x \to 0^-} x \cdot \frac{\ln(1-x^2)}{\frac{\sin^2 x}{\cos x}} = \lim_{x \to 0^-} \frac{x \ln(1-x^2) \cos x}{\sin^2 x}$.

We can rewrite this using standard limits $\lim_{u \to 0} \frac{\ln(1+u)}{u} = 1$ and $\lim_{v \to 0} \frac{\sin v}{v} = 1$:

$\lim_{x \to 0^-} \frac{\ln(1-x^2)}{-x^2} \cdot \frac{-x^2}{\sin^2 x} \cdot x \cos x = \lim_{x \to 0^-} \frac{\ln(1+(-x^2))}{-x^2} \cdot \left(\frac{x}{\sin x}\right)^2 \cdot (-x \cos x)$.

As $x \to 0$, $\frac{\ln(1+(-x^2))}{-x^2} \to 1$, $\frac{x}{\sin x} \to 1$, and $-x \cos x \to 0$.

So, $\lim_{x \to 0^-} f(x) = 1 \cdot 1^2 \cdot 0 = 0$.

Since $\lim_{x \to 0^-} f(x) = \lim_{x \to 0^+} f(x) = f(0) = 0$, the function is continuous at $x=0$ for all values of $k$.

Step 2: Check for differentiability at $x=0$.

For differentiability at $x=0$, the left-hand derivative $f'(0^-)$ must be equal to the right-hand derivative $f'(0^+)$.

$f'(0^+) = \lim_{h \to 0^+} \frac{f(0+h) - f(0)}{h} = \lim_{h \to 0^+} \frac{(k^2 - 3k - 1)\sin h + h^2 - 0}{h}$

$= \lim_{h \to 0^+} \left( (k^2 - 3k - 1)\frac{\sin h}{h} + h \right) = (k^2 - 3k - 1) \cdot 1 + 0 = k^2 - 3k - 1$.

$f'(0^-) = \lim_{h \to 0^-} \frac{f(0+h) - f(0)}{h} = \lim_{h \to 0^-} \frac{h \frac{\ln(1+h)+\ln(1-h)}{\sec h - \cos h}}{h}$

$= \lim_{h \to 0^-} \frac{\ln(1+h)+\ln(1-h)}{\sec h - \cos h} = \lim_{h \to 0^-} \frac{\ln(1-h^2)}{\frac{\sin^2 h}{\cos h}} = \lim_{h \to 0^-} \frac{\ln(1-h^2) \cos h}{\sin^2 h}$.

We can evaluate this limit using Taylor series expansions around $h=0$:

$\ln(1-h^2) = -h^2 - \frac{(-h^2)^2}{2} - \dots = -h^2 - \frac{h^4}{2} - \dots$

$\cos h = 1 - \frac{h^2}{2!} + \dots$

$\sin h = h - \frac{h^3}{3!} + \dots \implies \sin^2 h = (h - \frac{h^3}{6} + \dots)^2 = h^2 - \frac{h^4}{3} + \dots$

So, $f'(0^-) = \lim_{h \to 0^-} \frac{(-h^2 - \frac{h^4}{2} - \dots)(1 - \frac{h^2}{2} + \dots)}{(h^2 - \frac{h^4}{3} + \dots)} = \lim_{h \to 0^-} \frac{-h^2(1 + \frac{h^2}{2} + \dots)(1 - \frac{h^2}{2} + \dots)}{h^2(1 - \frac{h^2}{3} + \dots)}$

$= \lim_{h \to 0^-} \frac{-(1 + O(h^2))}{1 - \frac{h^2}{3} + \dots} = \frac{-1}{1} = -1$.

Alternatively, using L'Hopital's Rule on $\lim_{h \to 0} \frac{\ln(1-h^2) \cos h}{\sin^2 h}$:

Let $L = \lim_{h \to 0} \frac{\ln(1-h^2) \cos h}{\sin^2 h}$. This is of the form $\frac{0}{0}$.

Using L'Hopital's rule:

Numerator derivative: $\frac{-2h}{1-h^2} \cos h + \ln(1-h^2)(-\sin h)$.

Denominator derivative: $2 \sin h \cos h = \sin(2h)$.

$L = \lim_{h \to 0} \frac{\frac{-2h \cos h}{1-h^2} - \ln(1-h^2)\sin h}{\sin(2h)}$. This is still $\frac{0}{0}$.

Using L'Hopital's rule again:

Numerator second derivative (evaluated at $h=0$):

Derivative of $\frac{-2h \cos h}{1-h^2}$: $\frac{(-2 \cos h + 2h \sin h)(1-h^2) - (-2h \cos h)(-2h)}{(1-h^2)^2}$. At $h=0$, this is $\frac{(-2)(1) - 0}{1^2} = -2$.

Derivative of $-\ln(1-h^2)\sin h$: $-[\frac{-2h}{1-h^2}\sin h + \ln(1-h^2)\cos h]$. At $h=0$, this is $-[0 + 0] = 0$.

So, the second derivative of the numerator at $h=0$ is $-2 + 0 = -2$.

Second derivative of denominator $\sin(2h)$: $2 \cos(2h)$. At $h=0$, this is $2 \cos(0) = 2$.

So, $L = \frac{-2}{2} = -1$.

Thus, $f'(0^-) = -1$.

For differentiability at $x=0$, we must have $f'(0^+) = f'(0^-)$:

$k^2 - 3k - 1 = -1$.

$k^2 - 3k = 0$.

$k(k - 3) = 0$.

The two values of $k$ for which the function is differentiable at $x=0$ are $k_1 = 0$ and $k_2 = 3$.

We are asked to find the value of $(k_1^2 + k_2^2 - 3)$.

$(0^2 + 3^2 - 3) = (0 + 9 - 3) = 6$.

The final answer is $\boxed{6}$.