Question
Question: $$-\frac{1}{3} \leq |3x-4| \leq 2$$...
−31≤∣3x−4∣≤2
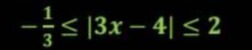
Answer
32≤x≤2
Explanation
Solution
The inequality −31≤∣3x−4∣≤2 implies two conditions:
- ∣3x−4∣≥−31: This is true for all x∈R since ∣3x−4∣≥0.
- ∣3x−4∣≤2: This is equivalent to −2≤3x−4≤2. Adding 4 to all parts gives 2≤3x≤6. Dividing by 3 yields 32≤x≤2. The solution is the intersection of these conditions, which is 32≤x≤2.
