Question
Question: الشكل يوضح مجموعة من البوابات المنطقية متصلة معا. ...
الشكل يوضح مجموعة من البوابات المنطقية متصلة معا.
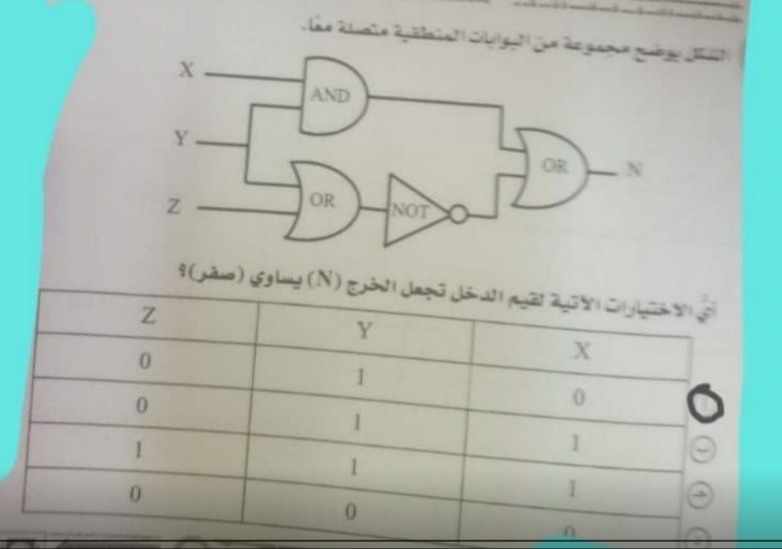
0 | 1 | 0
0 | 1 | 1
1 | 1 | 1
0 | 0 | 0
0 | 1 | 0
Solution
The problem asks us to find the input values (X, Y, Z) that make the output (N) of the given logic circuit equal to zero.
First, let's analyze the circuit and write down the Boolean expression for the output N.
-
AND gate: The inputs are X and Y. Let the output of this gate be P. P=X⋅Y
-
First OR gate: The inputs are Y and Z. Let the output of this gate be Q. Q=Y+Z
-
NOT gate: The input is Q. Let the output of this gate be R. R=Q=Y+Z
-
Second OR gate: The inputs are P and R. The output of this gate is N. N=P+R Substitute the expressions for P and R: N=(X⋅Y)+(Y+Z)
We want to find the input values (X, Y, Z) for which N=0. For an OR gate to output 0, both of its inputs must be 0. Therefore, we need:
- X⋅Y=0
- Y+Z=0
Let's analyze these two conditions:
-
Condition 1: X⋅Y=0 For an AND gate to output 0, at least one of its inputs must be 0. So, either X must be 0, or Y must be 0, or both.
-
Condition 2: Y+Z=0 This implies Y+Z=1. For an OR gate to output 1, at least one of its inputs must be 1. So, either Y must be 1, or Z must be 1, or both.
Now, let's test each option given in the table:
Option 1: X=0, Y=1, Z=0
- Check Condition 1 (X⋅Y=0): 0⋅1=0. (Satisfied)
- Check Condition 2 (Y+Z=1): 1+0=1. (Satisfied) Since both conditions are satisfied, this set of inputs will result in N=0.
Let's verify the output N for this option: P=X⋅Y=0⋅1=0 Q=Y+Z=1+0=1 R=Q=1=0 N=P+R=0+0=0. This option is correct.
Let's quickly check the other options to confirm they don't give N=0.
Option 2: X=1, Y=1, Z=0
- Check Condition 1 (X⋅Y=0): 1⋅1=1. (Not satisfied) Since X⋅Y=1, the first input to the final OR gate is 1. Thus, N will be 1, regardless of the second input. N=(1)+(1+0)=1+1=1+0=1. This option is incorrect.
Option 3: X=1, Y=1, Z=1
- Check Condition 1 (X⋅Y=0): 1⋅1=1. (Not satisfied) N=(1)+(1+1)=1+1=1+0=1. This option is incorrect.
Option 4: X=0, Y=0, Z=0
- Check Condition 2 (Y+Z=1): 0+0=0. (Not satisfied) Since Y+Z=0, then Y+Z=1. So the second input to the final OR gate is 1. Thus, N will be 1, regardless of the first input. N=(0⋅0)+(0+0)=0+0=0+1=1. This option is incorrect.
Therefore, only the first option (X=0, Y=1, Z=0) results in an output N equal to zero.
