Question
Question: Solve the inequality $\frac{(x-2)^{10000}(x+1)^{253}(x-\frac{1}{2})^{971}(x+8)^4}{x^{500}(x-3)^{75}...
Solve the inequality
x500(x−3)75(x+2)93(x−2)10000(x+1)253(x−21)971(x+8)4≥0
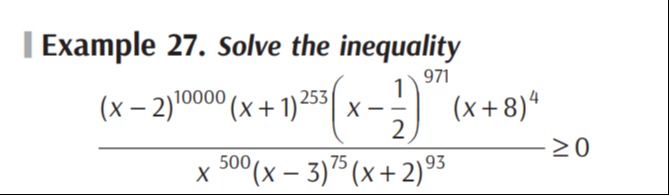
(−∞,−2)∪[−1,0)∪(0,21]∪{2}∪(3,∞)
Solution
To solve the inequality x500(x−3)75(x+2)93(x−2)10000(x+1)253(x−21)971(x+8)4≥0, we use the sign chart method.
1. Find the Critical Points:
Set each factor in the numerator and denominator to zero:
- From numerator:
- x−2=0⇒x=2 (even power: 10000)
- x+1=0⇒x=−1 (odd power: 253)
- x−21=0⇒x=21 (odd power: 971)
- x+8=0⇒x=−8 (even power: 4)
- From denominator:
- x=0⇒x=0 (even power: 500)
- x−3=0⇒x=3 (odd power: 75)
- x+2=0⇒x=−2 (odd power: 93)
List all critical points in increasing order: −8,−2,−1,0,21,2,3.
2. Analyze the Effect of Powers:
- Odd powers: At roots corresponding to factors with odd powers, the sign of the expression changes. These are x=−1,x=21,x=−2,x=3.
- Even powers: At roots corresponding to factors with even powers, the sign of the expression does not change. These are x=2,x=−8,x=0.
- Denominator roots: Points x=0,x=3,x=−2 make the denominator zero, so the expression is undefined at these points. They must always be excluded from the solution.
- Numerator roots: Points x=2,x=−1,x=21,x=−8 make the expression zero. Since the inequality is ≥0, these points are included in the solution if they are not denominator roots.
3. Determine the Sign in Intervals (Sign Chart):
Start with the rightmost interval (3,∞). Let x=4:
All factors (x−2),(x+1),(x−21),(x+8),x,(x−3),(x+2) are positive.
So, (+)500(+)75(+)93(+)10000(+)253(+)971(+)4=(+)≥0.
Thus, f(x)>0 for x∈(3,∞).
Now, move left across the critical points, changing sign only at odd-powered roots:
| Interval | Test Point | Sign of f(x) | Reason for sign change/no change |
|---|---|---|---|
| (3,∞) | x=4 | + | (Starting point) |
| x=3 | Undefined | Odd power (75), denominator root | |
| (2,3) | x=2.5 | − | Sign changes at x=3 |
| x=2 | 0 | Even power (10000), numerator root. Sign does not change across x=2. | |
| (21,2) | x=1 | − | Sign does not change at x=2 |
| x=21 | 0 | Odd power (971), numerator root. Sign changes across x=21. | |
| (0,21) | x=0.1 | + | Sign changes at x=21 |
| x=0 | Undefined | Even power (500), denominator root. Sign does not change across x=0. | |
| (−1,0) | x=−0.5 | + | Sign does not change at x=0 |
| x=−1 | 0 | Odd power (253), numerator root. Sign changes across x=−1. | |
| (−2,−1) | x=−1.5 | − | Sign changes at x=−1 |
| x=−2 | Undefined | Odd power (93), denominator root. Sign changes across x=−2. | |
| (−8,−2) | x=−3 | + | Sign changes at x=−2 |
| x=−8 | 0 | Even power (4), numerator root. Sign does not change across x=−8. | |
| (−∞,−8) | x=−9 | + | Sign does not change at x=−8 |
4. Formulate the Solution Set:
We need f(x)≥0. This means f(x)>0 or f(x)=0.
-
Intervals where f(x)>0: (−∞,−8), (−8,−2), (−1,0), (0,21), (3,∞).
-
Points where f(x)=0 (numerator roots): x=−8,x=−1,x=21,x=2.
-
Points where f(x) is undefined (denominator roots): x=−2,x=0,x=3. These must be excluded.
Combine the intervals and points:
- From (−∞,−8) and x=−8 and (−8,−2): This combines to (−∞,−2). (Note: x=−2 is excluded).
- From (−1,0) and x=−1: This combines to [−1,0). (Note: x=0 is excluded).
- From (0,21) and x=21: This combines to (0,21]. (Note: x=0 is excluded).
- The point x=2 makes f(x)=0, and it's not excluded by the denominator. So, x=2 is an isolated solution.
- From (3,∞): This is an interval where f(x)>0. (Note: x=3 is excluded).
The final solution is the union of these parts:
x∈(−∞,−2)∪[−1,0)∪(0,21]∪{2}∪(3,∞).
