Question

If a, b, c, d, e are positive real numbers, such that

$a+b+c+d+e=8$ and $a^2 + b^2+c^2 + d^2 + e^2 = 16$, find the range of e.

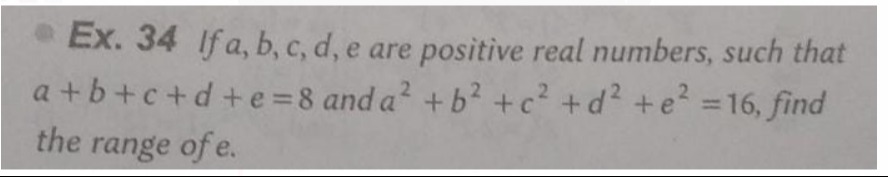
Answer 1

e ∈ (0, 16/5]

Answer 2

We are given:

$$a+b+c+d+e=8 \quad \text{and} \quad a^2+b^2+c^2+d^2+e^2=16,$$

with $a,b,c,d,e>0$.

Let

$$S = a+b+c+d = 8 - e,\quad T = a^2+b^2+c^2+d^2 = 16 - e^2.$$

By the QM–AM inequality for the four positive numbers $a, b, c, d$,

$$\sqrt{\frac{T}{4}} \ge \frac{S}{4}.$$

Squaring both sides,

$$\frac{T}{4} \ge \left(\frac{S}{4}\right)^2 \quad\Rightarrow\quad 4T \ge S^2.$$

Substitute $T$ and $S$:

$$4(16 - e^2) \ge (8-e)^2.$$

Expanding both sides:

$$64 - 4e^2 \ge 64 - 16e + e^2.$$

Bring all terms to one side:

$$64 - 4e^2 - 64 + 16e - e^2 \ge 0 \quad\Rightarrow\quad -5e^2 + 16e \ge 0.$$

Multiply by $-1$ (reversing the inequality):

$$5e^2 - 16e \le 0 \quad\Rightarrow\quad e(5e - 16) \le 0.$$

Thus, the inequality holds when:

$$0 \le e \le \frac{16}{5}.$$

Since $e > 0$ (positivity condition), the range is

$$0 < e \le \frac{16}{5}.$$

We also note that the upper bound $e=\frac{16}{5}$ is attainable by choosing

$$a=b=c=d=\frac{8-\frac{16}{5}}{4}=\frac{6}{5},$$

which are positive. The lower bound is not attained because if $e=0$ then $e$ is not positive; however, values of $e$ can get arbitrarily close to $0$.

Answer:
$e \in \left(0, \frac{16}{5}\right]$.