Question

The joint equation of pair of lines through (2, 3) and perpendicular to the coordinate axes is

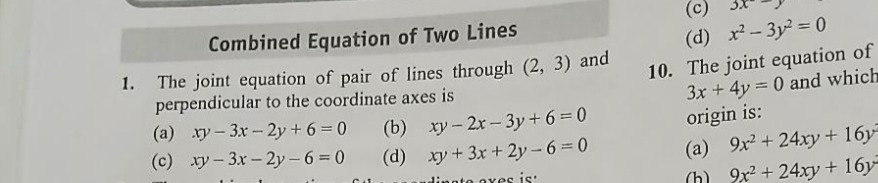
• A. $xy - 3x - 2y + 6 = 0$
• B. $xy - 2x - 3y + 6 = 0$
• C. $xy - 3x - 2y - 6 = 0$
• D. $xy + 3x + 2y - 6 = 0$

Answer 1

Answer: (A)

(a) $xy - 3x - 2y + 6 = 0$

Answer 2

For a pair of lines through (2, 3) which are perpendicular to the coordinate axes the lines are:

• vertical: $x = 2$

• horizontal: $y = 3$

Their combined (joint) equation is obtained by writing:

$(x-2)(y-3)=0 \implies xy-3x-2y+6=0$.