Question

A block of 200 g mass moves with a uniform speed in a horizontal circular groove, with vertical side walls of radius 20 cm. If the block takes 40 s to complete one round, the normal force by the side walls of the groove is ($\pi^2 \approx 10$)

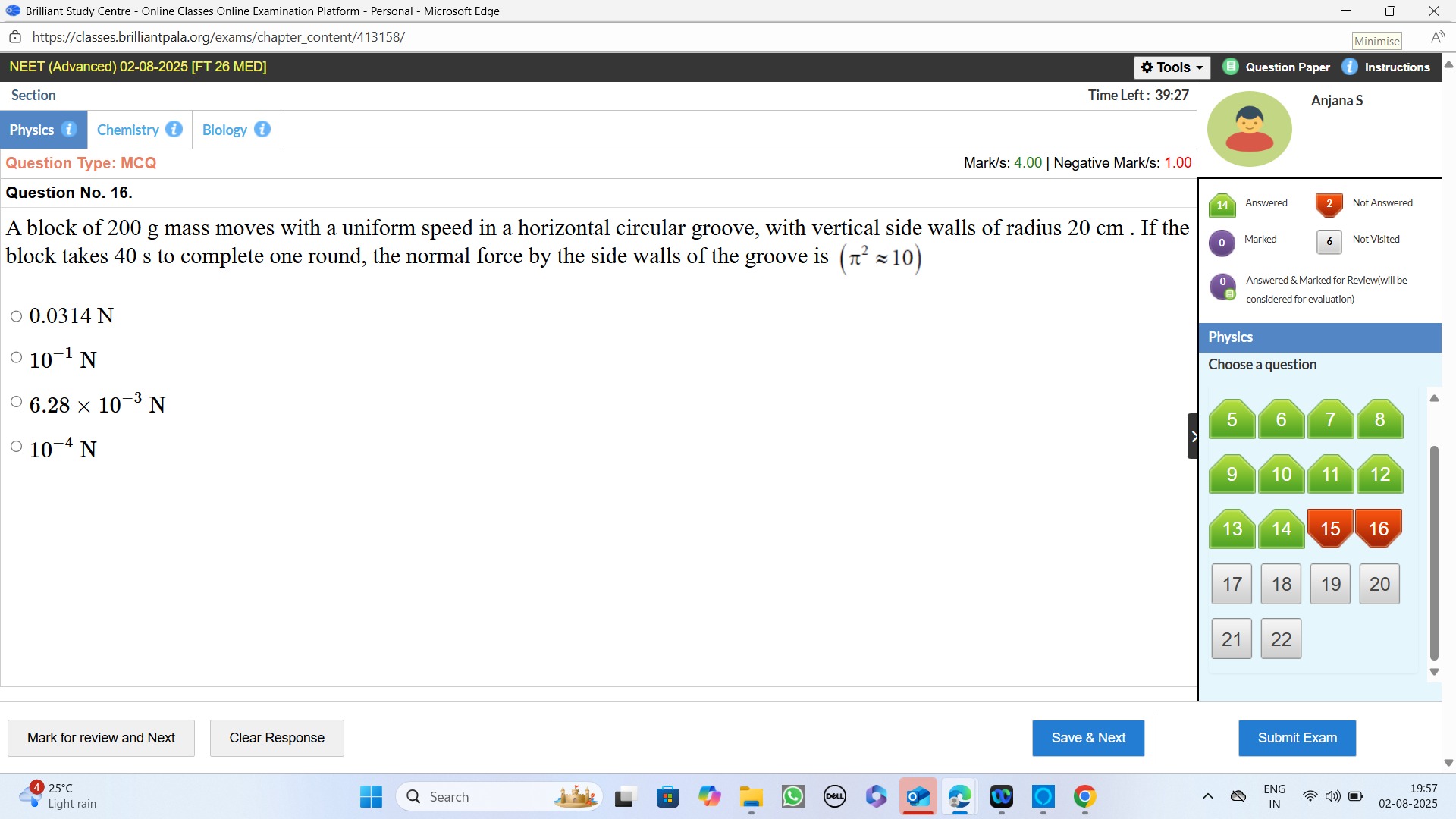
• A. 0.0314 N
• B. $10^{-1}$ N
• C. 6.28 × $10^{-3}$ N
• D. $10^{-4}$ N

Answer 1

0.001 N (Not among the options provided. There might be an error in the question or options.)

Answer 2

The normal force by the side walls of the groove is equal to the centripetal force required for the circular motion.

Given:

• Mass, $m = 200 \text{ g} = 0.2 \text{ kg}$
• Radius, $r = 20 \text{ cm} = 0.2 \text{ m}$
• Time period, $T = 40 \text{ s}$
• $\pi^2 \approx 10$

The centripetal force $F_c$ is given by:

$F_c = m \omega^2 r = m \left(\frac{2\pi}{T}\right)^2 r = m \frac{4\pi^2 r}{T^2}$

Substituting the values:

$F_c = 0.2 \times \frac{4 \times 10 \times 0.2}{40^2} = 0.2 \times \frac{8}{1600} = \frac{1.6}{1600} = \frac{1}{1000} = 0.001 \text{ N}$

Therefore, the normal force is $0.001 \text{ N}$. This value is not among the given options, suggesting a possible error in the question or the provided options.