Question

A block of mass m slides on the wooden wedge, which in turn slides backward on the horizontal surface. The acceleration of the block with respect to the wedge is (Given m = 8 kg, M = 16 kg )

Assume all the surfaces shown in the figure to be frictionless

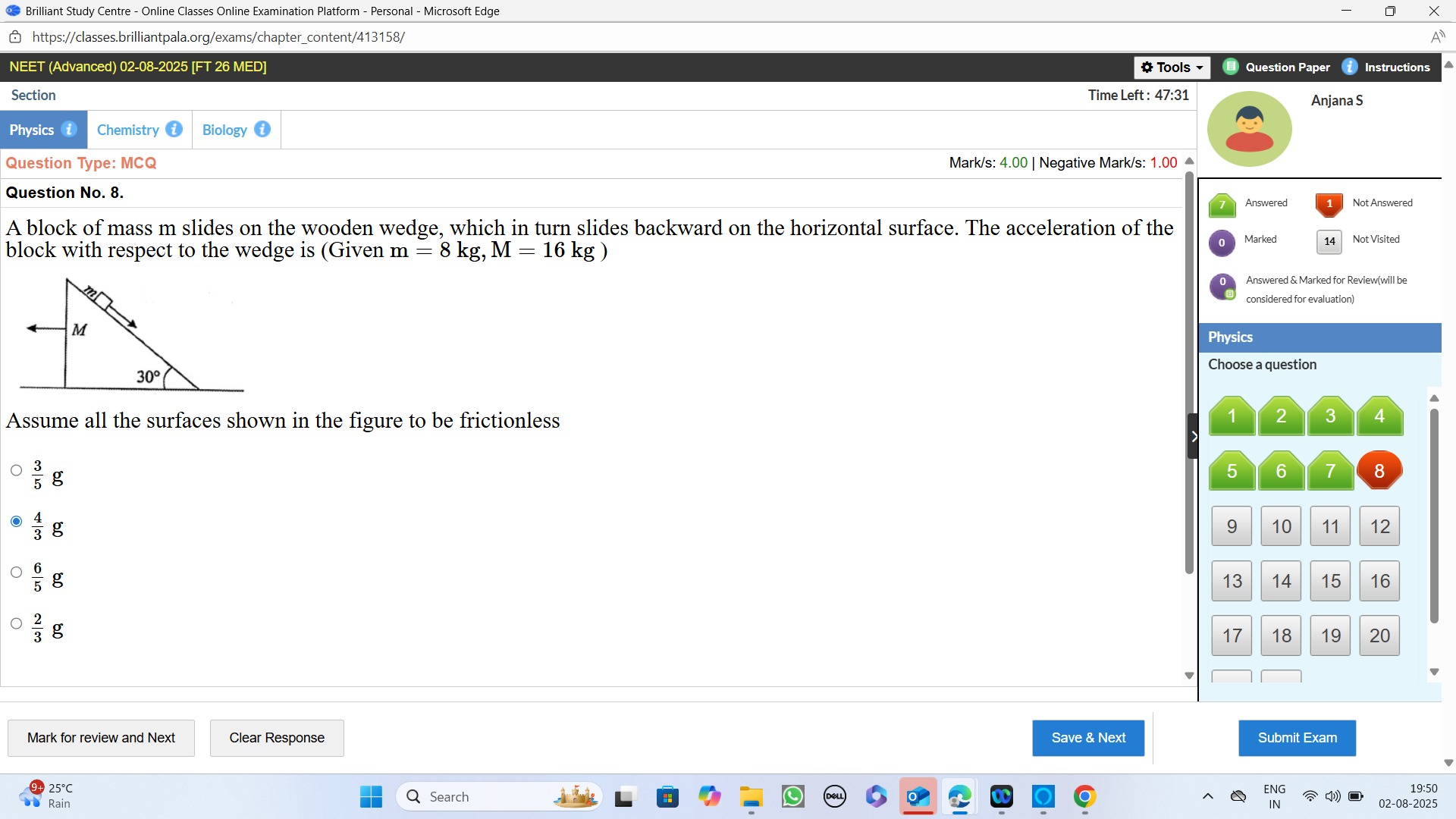
• A. $\frac{3}{5}g$
• B. $\frac{4}{3}g$
• C. $\frac{6}{5}g$
• D. $\frac{2}{3}g$

Answer 1

Answer: (D)

$\frac{2}{3}g$

Answer 2

Let $m$ be the mass of the block, $M$ be the mass of the wedge, and $\theta$ be the angle of inclination. The acceleration of the block with respect to the wedge, $a_{rel}$, on a frictionless surface is given by the formula:

$a_{rel} = \frac{g (M+m) \sin \theta}{M + m \sin^2 \theta}$

Given values: $m = 8$ kg $M = 16$ kg $\theta = 30^\circ$

Substitute the values into the formula: $\sin 30^\circ = \frac{1}{2}$ $\sin^2 30^\circ = \left(\frac{1}{2}\right)^2 = \frac{1}{4}$

$a_{rel} = \frac{g (16+8) \left(\frac{1}{2}\right)}{16 + 8 \left(\frac{1}{4}\right)}$ $a_{rel} = \frac{g (24) \left(\frac{1}{2}\right)}{16 + 2}$ $a_{rel} = \frac{12g}{18}$ $a_{rel} = \frac{2}{3}g$