Question
Question: Three concentric metal shells $A, B$ and $C$ of respective radii $a, b$ and $c(a < b < c)$ have surf...
Three concentric metal shells A,B and C of respective radii a,b and c(a<b<c) have surface charge densities +σ,−σ and +σ respectively. The potential of shell B is:
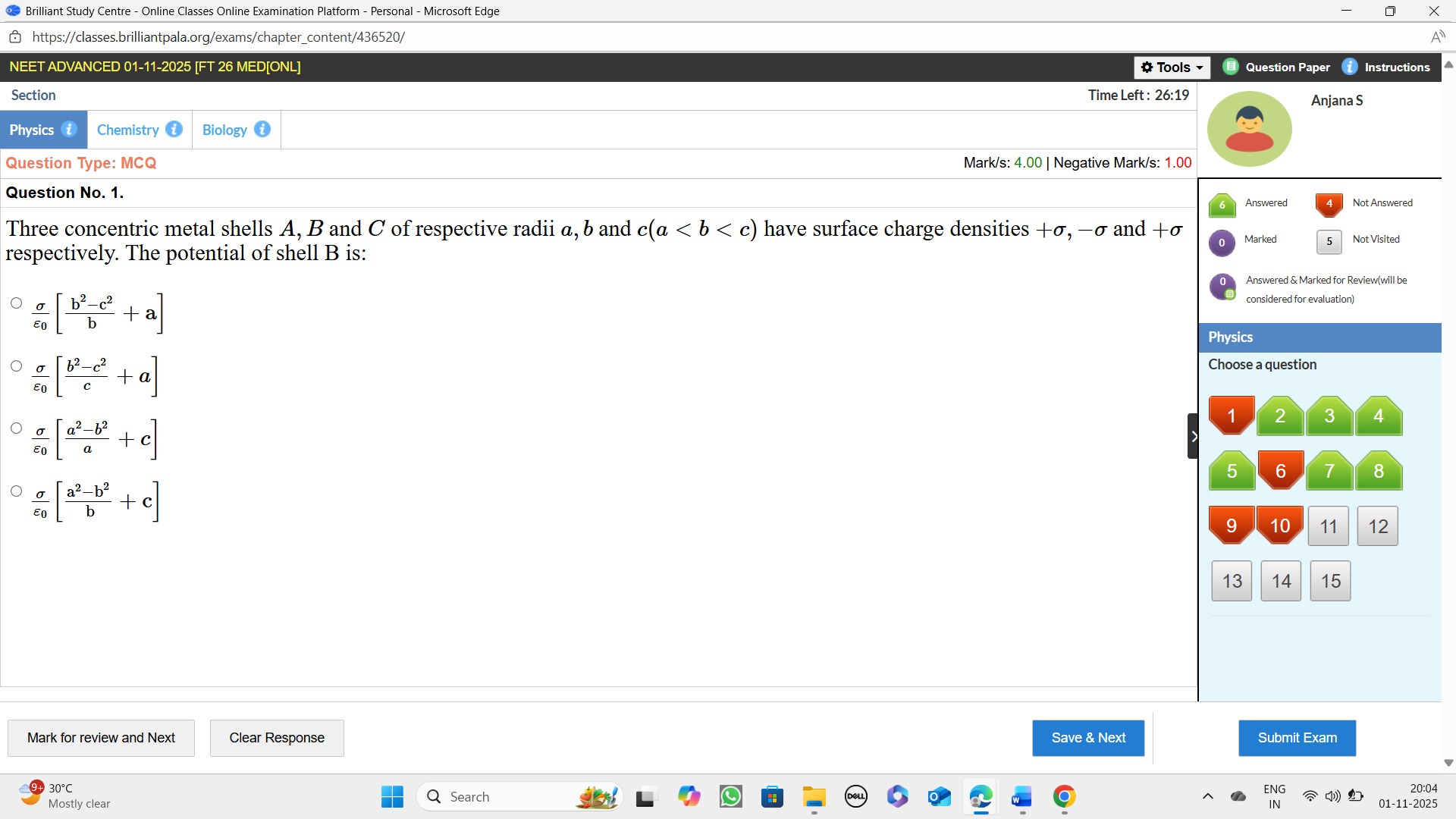
ϵ0σ[bb2−c2+a]
ϵ0σ[cb2−c2+a]
ϵ0σ[aa2−b2+c]
ϵ0σ[ba2−b2+c]
ϵ0σ[ba2−b2+c]
Solution
The potential at radius b is the sum of potentials due to each shell. Charge on shell A: QA=σ⋅4πa2 Charge on shell B: QB=−σ⋅4πb2 Charge on shell C: QC=σ⋅4πc2
Potential at radius b due to shell A (since b>a): VA=bkQA=4πϵ01bσ⋅4πa2=ϵ0bσa2 Potential at radius b due to shell B (since b is on the surface): VB=bkQB=4πϵ01b−σ⋅4πb2=−ϵ0bσb2=−ϵ0σb Potential at radius b due to shell C (since b<c): VC=ckQC=4πϵ01cσ⋅4πc2=ϵ0cσc2=ϵ0σc
Total potential at b: VB=VA+VB+VC=ϵ0bσa2−ϵ0σb+ϵ0σc=ϵ0σ(ba2−b+c)=ϵ0σ(ba2−b2+c).
