Question

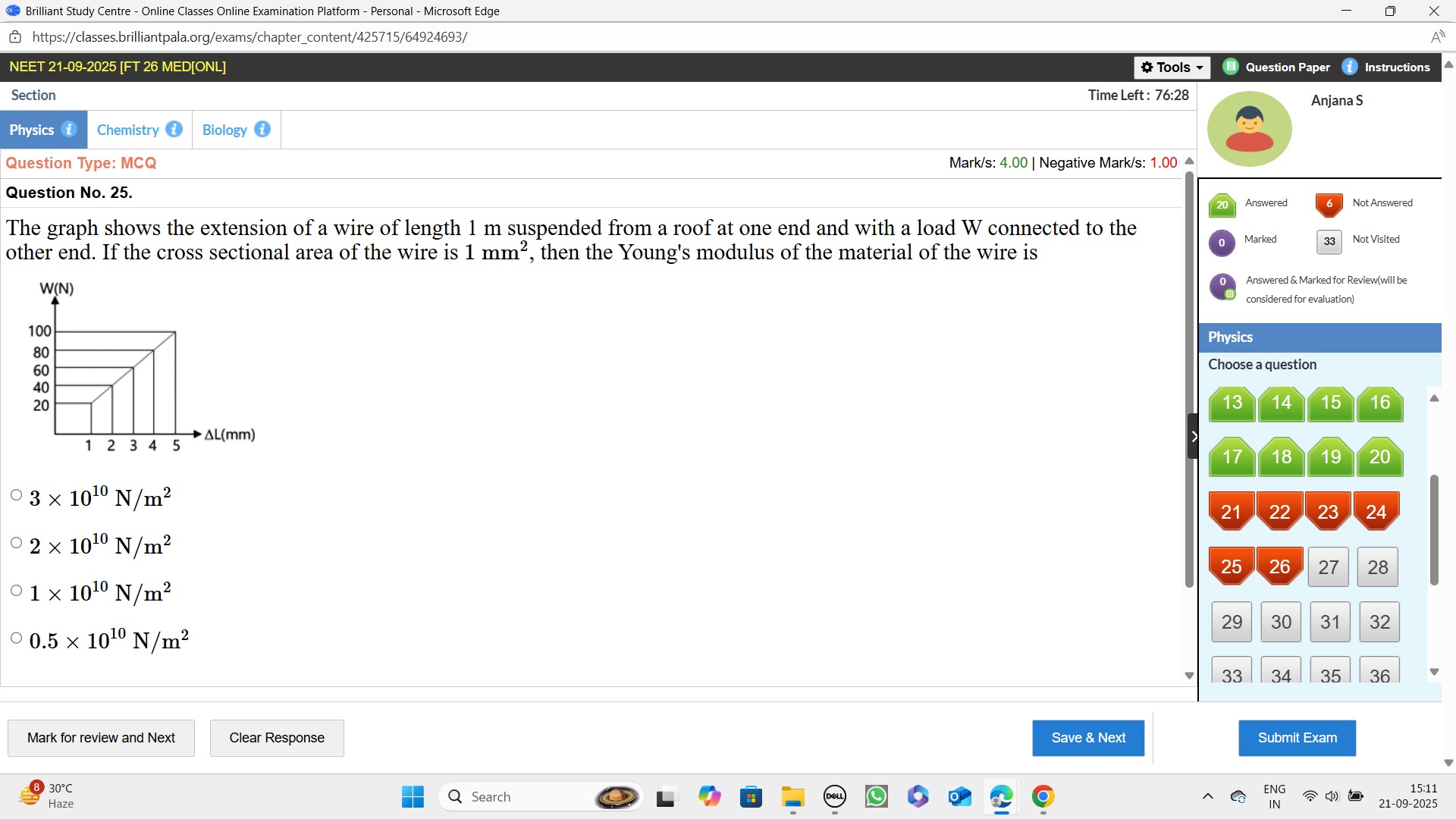
The graph shows the extension of a wire of length 1 m suspended from a roof at one end and with a load W connected to the other end. If the cross sectional area of the wire is $1 mm^2$, then the Young's modulus of the material of the wire is

• A. $3 \times 10^{10} N/m^2$
• B. $2 \times 10^{10} N/m^2$
• C. $1 \times 10^{10} N/m^2$
• D. $0.5 \times 10^{10} N/m^2$

Answer 1

Answer: (B)

$2 \times 10^{10} N/m^2$

Answer 2

Young's modulus ($Y$) is defined as the ratio of stress to strain: $Y = \frac{\text{Stress}}{\text{Strain}}$ where Stress $= \frac{F}{A}$ and Strain $= \frac{\Delta L}{L}$. Thus, the formula for Young's modulus is: $Y = \frac{F \cdot L}{A \cdot \Delta L}$ From the given graph, we can pick a point. Let's choose the point where the load $W = 100$ N and the extension $\Delta L = 5$ mm. Given:

• Original length of the wire, $L = 1$ m.
• Cross-sectional area of the wire, $A = 1$ mm$^2$. Convert to m$^2$: $A = 1 \times (10^{-3} \text{ m})^2 = 1 \times 10^{-6}$ m$^2$.
• Load, $F = W = 100$ N.
• Extension, $\Delta L = 5$ mm. Convert to m: $\Delta L = 5 \times 10^{-3}$ m.

Substitute these values into the Young's modulus formula: $Y = \frac{(100 \text{ N}) \cdot (1 \text{ m})}{(1 \times 10^{-6} \text{ m}^2) \cdot (5 \times 10^{-3} \text{ m})}$ $Y = \frac{100}{5 \times 10^{-9}} \text{ N/m}^2$ $Y = 20 \times 10^9 \text{ N/m}^2$ $Y = 2 \times 10^{10} \text{ N/m}^2$