Question

For the reaction, $Fe_3N(s) + \frac{3}{2}H_2(g) \rightleftharpoons 3Fe(s) + NH_3(g)$

• A. $K_c = K_p (RT)$
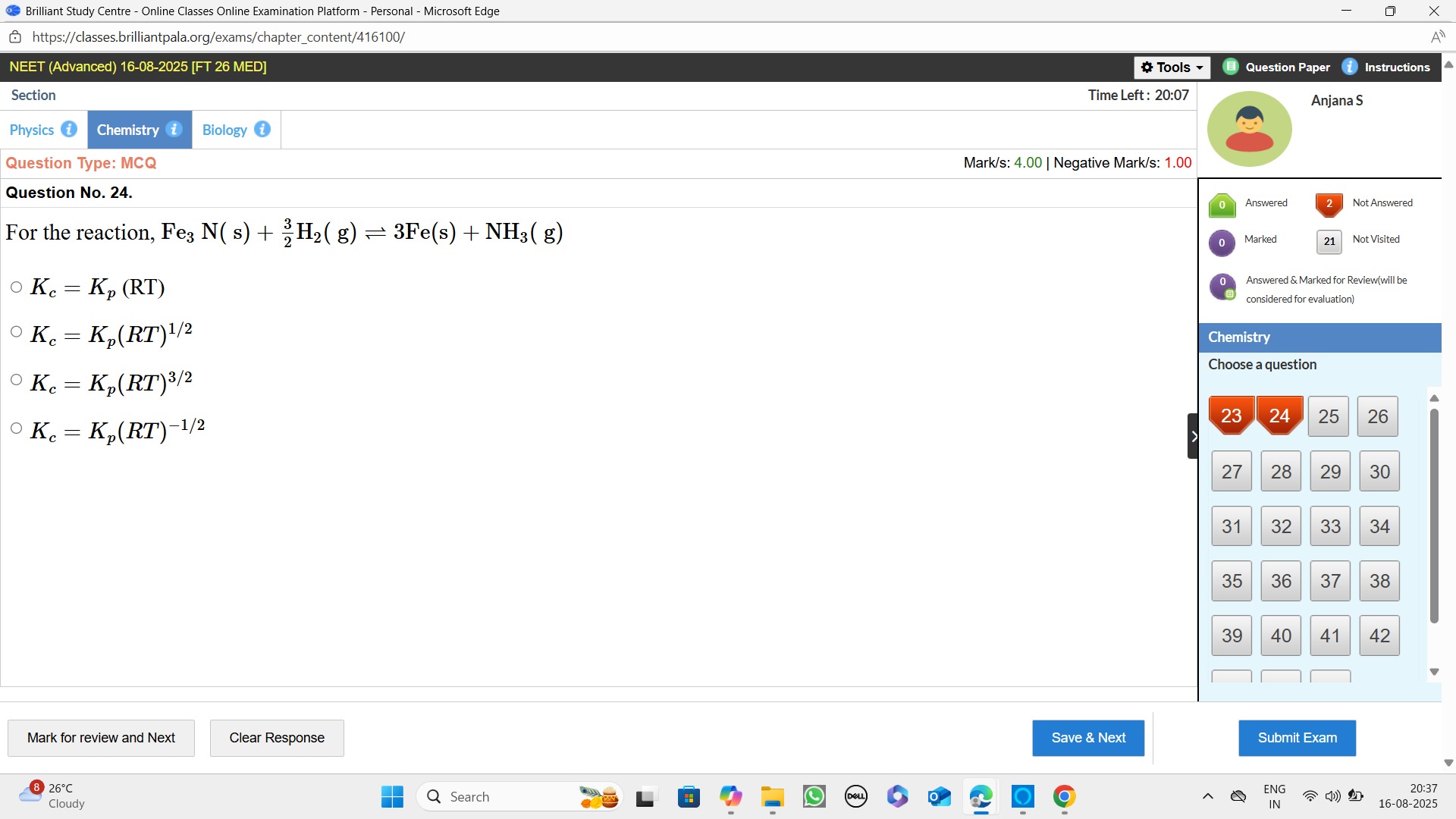
• B. $K_c = K_p (RT)^{1/2}$
• C. $K_c = K_p (RT)^{3/2}$
• D. $K_c = K_p (RT)^{-1/2}$

Answer 1

Answer: (B)

$K_c = K_p (RT)^{1/2}$

Answer 2

The relationship between $K_p$ and $K_c$ for a reaction is given by the equation:

$K_p = K_c (RT)^{\Delta n_g}$

Where:

$K_p$ = Equilibrium constant in terms of partial pressures

$K_c$ = Equilibrium constant in terms of molar concentrations

$R$ = Ideal gas constant

$T$ = Absolute temperature in Kelvin

$\Delta n_g$ = (Sum of stoichiometric coefficients of gaseous products) - (Sum of stoichiometric coefficients of gaseous reactants)

The given reaction is:

$Fe_3N(s) + \frac{3}{2}H_2(g) \rightleftharpoons 3Fe(s) + NH_3(g)$

To calculate $\Delta n_g$, we only consider the gaseous species.

Moles of gaseous products ($n_{p,g}$):

For $NH_3(g)$, the stoichiometric coefficient is 1.

So, $n_{p,g} = 1$.

Moles of gaseous reactants ($n_{r,g}$):

For $H_2(g)$, the stoichiometric coefficient is $\frac{3}{2}$.

So, $n_{r,g} = \frac{3}{2}$.

Now, calculate $\Delta n_g$:

$\Delta n_g = n_{p,g} - n_{r,g}$

$\Delta n_g = 1 - \frac{3}{2}$

$\Delta n_g = \frac{2}{2} - \frac{3}{2}$

$\Delta n_g = -\frac{1}{2}$

Substitute the value of $\Delta n_g$ into the relationship between $K_p$ and $K_c$:

$K_p = K_c (RT)^{-1/2}$

The question asks for the relationship expressed in terms of $K_c$. Rearrange the equation:

$K_c = \frac{K_p}{(RT)^{-1/2}}$

$K_c = K_p (RT)^{1/2}$

Comparing this with the given options, the second option matches our derived relationship.