Question

A body is displaced from origin to ( 1 m, 1 m ) by a force $\overrightarrow{F}$ = $2y\hat{i} + 3x^2\hat{j}$ along to the path x = y

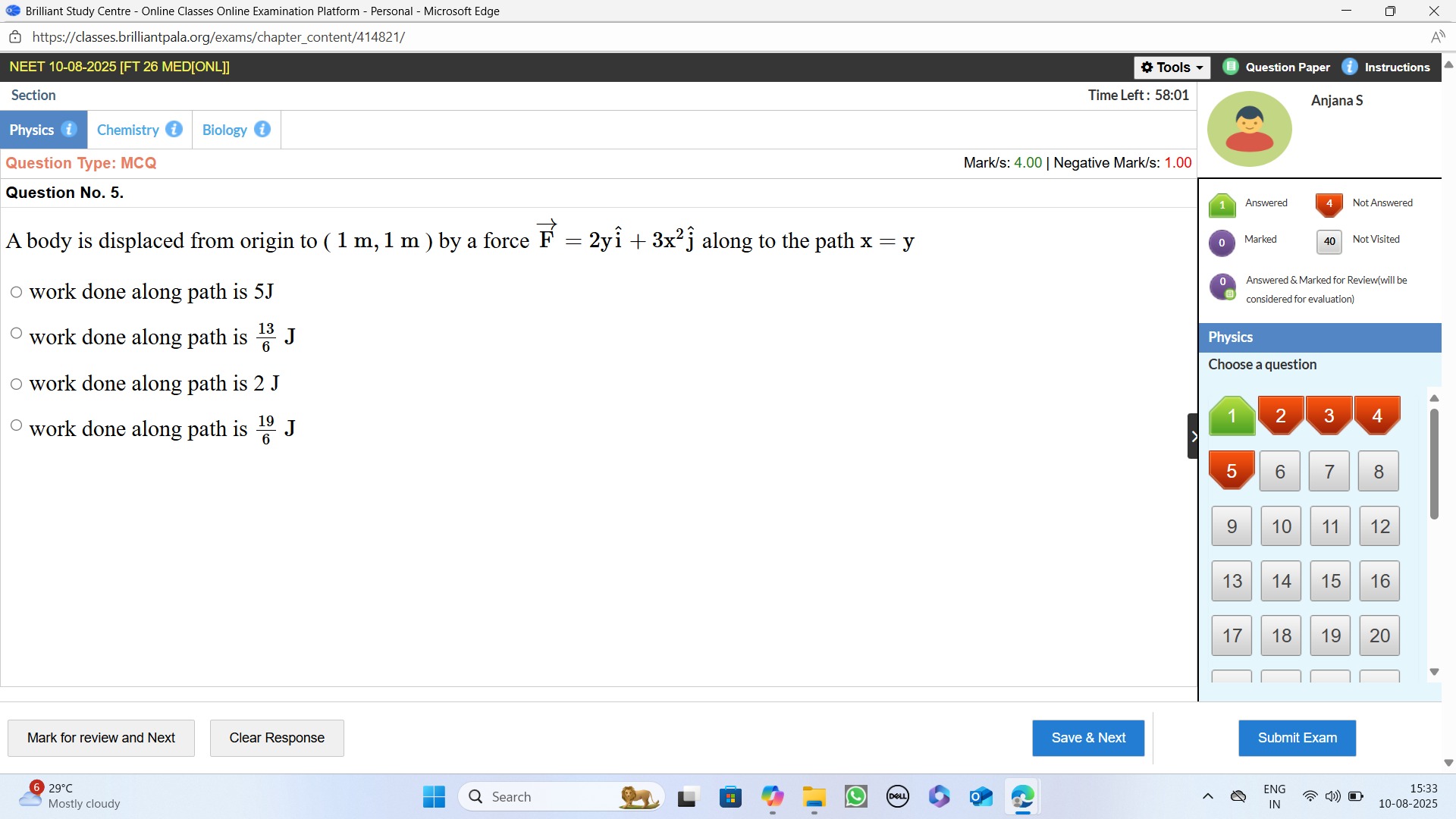
• A. work done along path is 5J
• B. work done along path is $\frac{13}{6}$ J
• C. work done along path is 2 J
• D. work done along path is $\frac{19}{6}$ J

Answer 1

Answer: (C)

work done along path is 2 J

Answer 2

The work done by a variable force $\vec{F}$ over a displacement $d\vec{r}$ is given by the line integral:

$W = \int \vec{F} \cdot d\vec{r}$

Given force: $\vec{F} = 2y\hat{i} + 3x^2\hat{j}$

Differential displacement: $d\vec{r} = dx\hat{i} + dy\hat{j}$

First, calculate the dot product $\vec{F} \cdot d\vec{r}$:

$\vec{F} \cdot d\vec{r} = (2y\hat{i} + 3x^2\hat{j}) \cdot (dx\hat{i} + dy\hat{j})$ $\vec{F} \cdot d\vec{r} = 2y \, dx + 3x^2 \, dy$

The body is displaced from the origin (0, 0) to (1m, 1m) along the path x = y. Since x = y, it implies that $dx = dy$.

Substitute y = x and dy = dx into the expression for work done:

$W = \int_{(0,0)}^{(1,1)} (2x \, dx + 3x^2 \, dx)$ $W = \int_{(0,0)}^{(1,1)} (2x + 3x^2) \, dx$

Since we have expressed the integrand solely in terms of x, the limits of integration for x will be from 0 to 1 (corresponding to the starting point x=0 and ending point x=1).

Now, perform the integration:

$W = \left[ \frac{2x^2}{2} + \frac{3x^3}{3} \right]_{0}^{1}$ $W = \left[ x^2 + x^3 \right]_{0}^{1}$

Evaluate the definite integral using the limits:

$W = (1^2 + 1^3) - (0^2 + 0^3)$ $W = (1 + 1) - (0)$ $W = 2 \text{ J}$

The work done along the path is 2 J.