Question

$S_2O_8^{2-}$(aq) oxidises $Mn^{2+}$(aq) to $MnO_4^-$ (aq) in acidic medium. The number of moles of $S_2O_8^{2-}$ required to oxidise one mole $Mn^{2+}$ to $MnO_4^-$ is

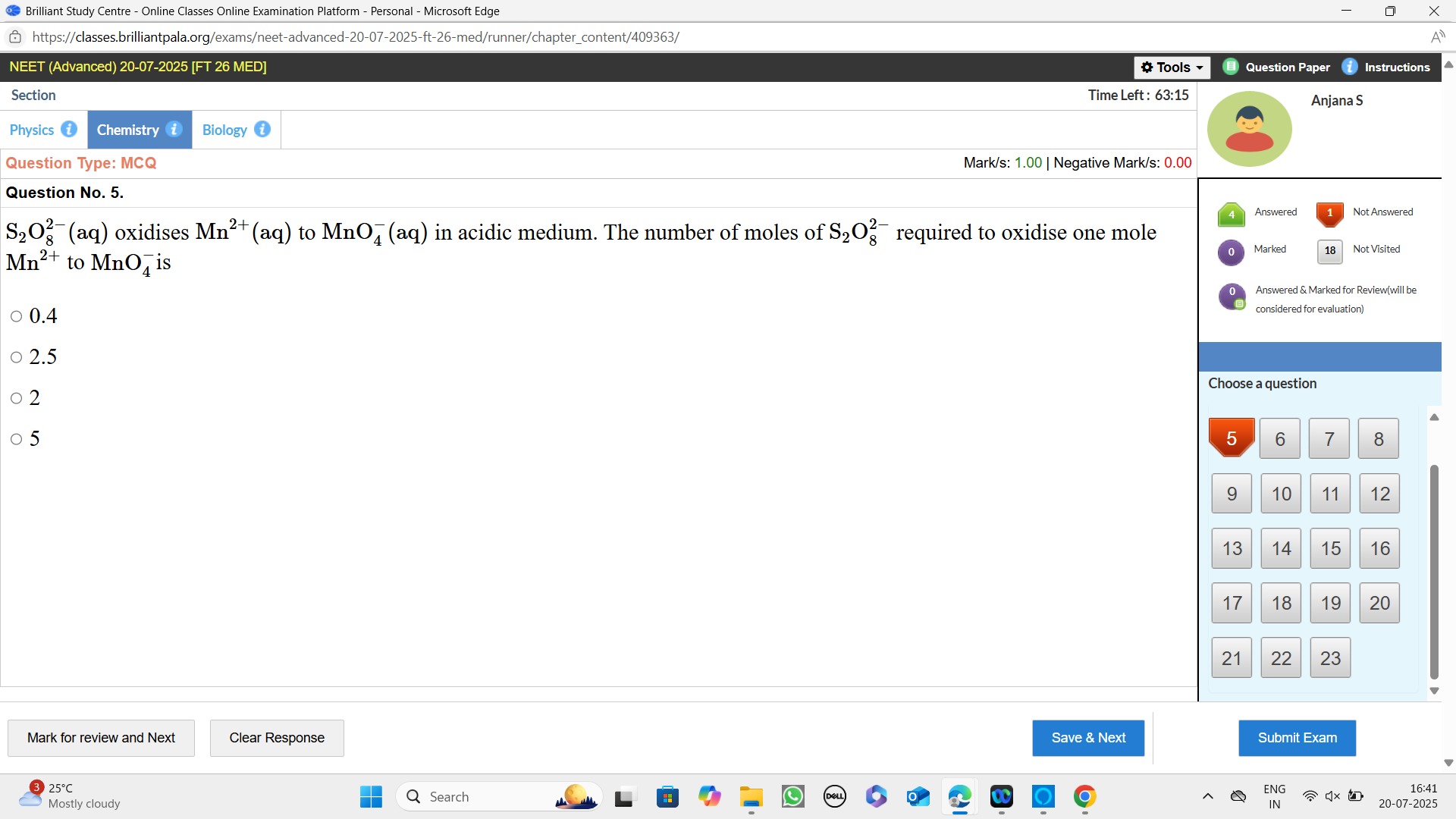
• A. 0.4
• B. 2.5
• C. 2
• D. 5

Answer 1

Answer: (B)

2.5

Answer 2

The problem asks for the number of moles of $S_2O_8^{2-}$ required to oxidize one mole of $Mn^{2+}$ to $MnO_4^-$ in an acidic medium. We can solve this by balancing the redox reaction or by using the concept of n-factors (equivalents).

Method 1: Balancing the Redox Reaction

1. Identify the oxidation and reduction half-reactions:

   • Oxidation: $Mn^{2+} \rightarrow MnO_4^-$
   • Reduction: $S_2O_8^{2-} \rightarrow SO_4^{2-}$

2. Balance the oxidation half-reaction: $Mn^{2+}$ has an oxidation state of +2. In $MnO_4^-$, Mn has an oxidation state of +7 (since $x + 4(-2) = -1 \Rightarrow x = +7$). The change in oxidation state for Mn is $7 - 2 = 5$. So, 5 electrons are lost. Balance oxygen atoms by adding $H_2O$ and hydrogen atoms by adding $H^+$ (acidic medium): $Mn^{2+} + 4H_2O \rightarrow MnO_4^- + 8H^+ + 5e^-$

3. Balance the reduction half-reaction: In $S_2O_8^{2-}$ (peroxodisulfate ion), the average oxidation state of sulfur is +7 (since $2x + 8(-2) = -2 \Rightarrow 2x = 14 \Rightarrow x = +7$). In $SO_4^{2-}$, sulfur has an oxidation state of +6 (since $y + 4(-2) = -2 \Rightarrow y = +6$). The change in oxidation state per sulfur atom is $7 - 6 = 1$. Since there are two sulfur atoms in $S_2O_8^{2-}$ that get reduced to $2SO_4^{2-}$, a total of $2 \times 1 = 2$ electrons are gained. Balance the sulfur atoms first: $S_2O_8^{2-} \rightarrow 2SO_4^{2-}$ Now, add electrons to balance the charge: $S_2O_8^{2-} + 2e^- \rightarrow 2SO_4^{2-}$

4. Equalize the number of electrons transferred: The oxidation half-reaction involves 5 electrons, and the reduction half-reaction involves 2 electrons. To balance the electrons, multiply the oxidation half-reaction by 2 and the reduction half-reaction by 5.

   • $2 \times (Mn^{2+} + 4H_2O \rightarrow MnO_4^- + 8H^+ + 5e^-)$

$2Mn^{2+} + 8H_2O \rightarrow 2MnO_4^- + 16H^+ + 10e^-$ * $5 \times (S_2O_8^{2-} + 2e^- \rightarrow 2SO_4^{2-})$

$5S_2O_8^{2-} + 10e^- \rightarrow 10SO_4^{2-}$

5. Add the balanced half-reactions:

$2Mn^{2+} + 8H_2O + 5S_2O_8^{2-} + 10e^- \rightarrow 2MnO_4^- + 16H^+ + 10e^- + 10SO_4^{2-}$ Cancel out the electrons:

$2Mn^{2+} (aq) + 5S_2O_8^{2-} (aq) + 8H_2O (l) \rightarrow 2MnO_4^- (aq) + 10SO_4^{2-} (aq) + 16H^+ (aq)$

6. Determine the mole ratio: From the balanced equation, 2 moles of $Mn^{2+}$ react with 5 moles of $S_2O_8^{2-}$. Therefore, for 1 mole of $Mn^{2+}$, the moles of $S_2O_8^{2-}$ required will be: Moles of $S_2O_8^{2-} = \frac{5 \text{ moles } S_2O_8^{2-}}{2 \text{ moles } Mn^{2+}} \times 1 \text{ mole } Mn^{2+} = 2.5 \text{ moles } S_2O_8^{2-}$

Method 2: Using n-factors (Equivalents Concept)

The number of equivalents of oxidant must be equal to the number of equivalents of reductant. Number of equivalents = number of moles $\times$ n-factor

1. Calculate the n-factor for $Mn^{2+}$:

$Mn^{2+} \rightarrow MnO_4^-$ Oxidation state change: +2 to +7. Number of electrons lost = 5. So, n-factor ($n_{Mn^{2+}}$) = 5.

2. Calculate the n-factor for $S_2O_8^{2-}$:

$S_2O_8^{2-} \rightarrow 2SO_4^{2-}$ This reaction involves the gain of 2 electrons per mole of $S_2O_8^{2-}$. So, n-factor ($n_{S_2O_8^{2-}}$) = 2.

3. Apply the equivalence principle: Moles of $S_2O_8^{2-}$ $\times n_{S_2O_8^{2-}}$ = Moles of $Mn^{2+}$ $\times n_{Mn^{2+}}$ Let 'x' be the moles of $S_2O_8^{2-}$ required.

$x \times 2 = 1 \times 5$

$2x = 5$

$x = \frac{5}{2} = 2.5$

Both methods yield the same result.

The balanced redox reaction is:

$2Mn^{2+} (aq) + 5S_2O_8^{2-} (aq) + 8H_2O (l) \rightarrow 2MnO_4^- (aq) + 10SO_4^{2-} (aq) + 16H^+ (aq)$

From the stoichiometry, 2 moles of $Mn^{2+}$ are oxidized by 5 moles of $S_2O_8^{2-}$. Therefore, 1 mole of $Mn^{2+}$ requires $\frac{5}{2} = 2.5$ moles of $S_2O_8^{2-}$.