Question

Liquid concrete is poured into the form shown has radius R. The form has width w normal to the diagram. Compute the magnitude of the vertical force exerted on the form by the concrete and specify its line of action.

Answer 1

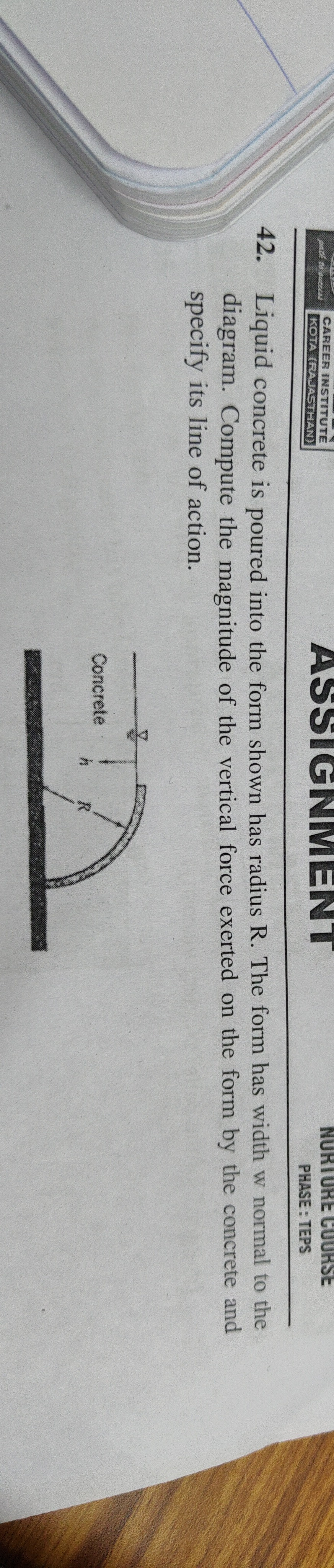
The magnitude of the vertical force exerted on the form by the concrete is $\frac{1}{4} \pi \rho g R^2 w$. The line of action of this force is the vertical line passing through the point located at a horizontal distance of $\frac{4R}{3\pi}$ from the vertical wall and a vertical distance of $\frac{4R}{3\pi}$ from the base, within the plane of the diagram.

Answer 2

The vertical force exerted by a liquid on a containing surface is equal to the weight of the liquid. The concrete fills a quarter-cylindrical volume of radius $R$ and width $w$. The volume of the concrete is $V = \frac{1}{4} \pi R^2 w$. Assuming the density of concrete is $\rho$ and acceleration due to gravity is $g$, the weight of the concrete is $W = \rho V g = \rho \frac{1}{4} \pi R^2 w g$. This weight is the magnitude of the vertical force exerted by the concrete on the form.

The line of action of this vertical force is the vertical line passing through the center of mass of the concrete. For a quarter-cylindrical volume, the center of mass has coordinates $(\frac{4R}{3\pi}, \frac{4R}{3\pi})$ relative to the center of curvature, assuming the quarter cylinder is oriented in the first octant with the center of curvature at the origin. Therefore, the line of action is the vertical line passing through the point $(\frac{4R}{3\pi}, \frac{4R}{3\pi})$ in the plane of the diagram.