Question

= (a cosC + b cosC) + ( b cos A + c cos A) + (c cos B + a cos B) = (a cos C + c cos A) + (b cos A + a cos B) + (c cos B + b cos C) = a + b + c =R.H.S.

Ex.(9) In $\triangle ABC$, prove that a(cos C - cos B) = 2(b - c) $\cos^2 (\frac{A}{2})$

Solution : By Projection rule, we have a cos C + c cos A = b and a cos B

$\therefore$ a cos C = b – c cos A and a cos B = c - b cos A

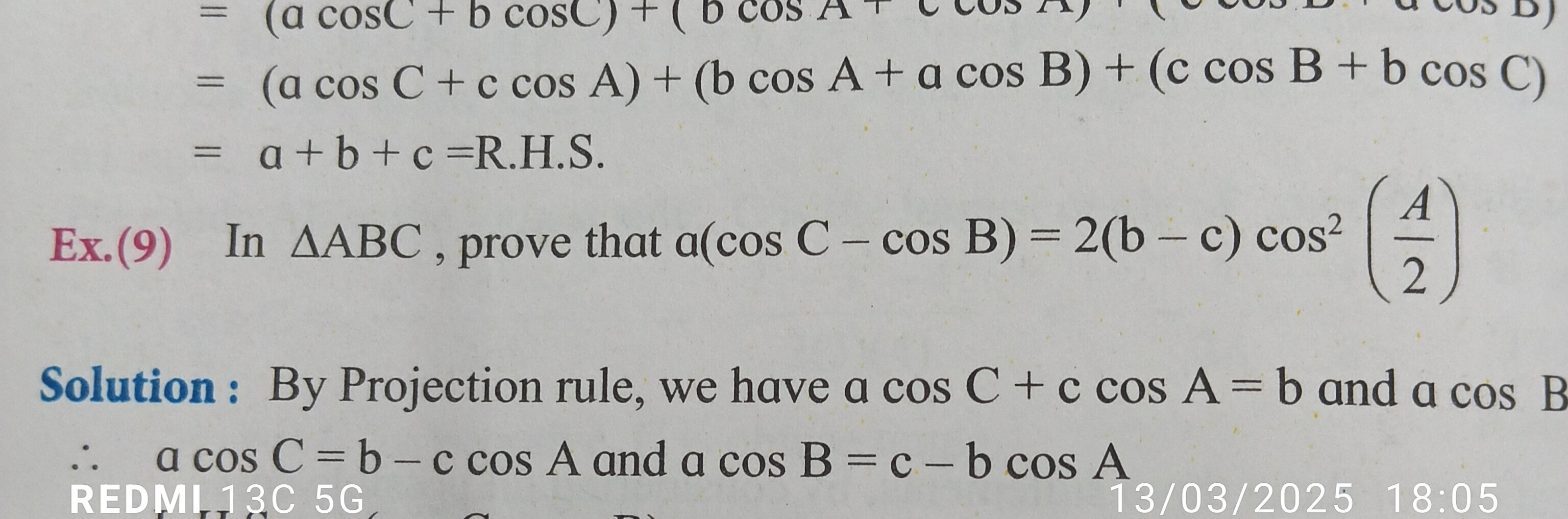
Answer 1

a(cos C - cos B)=2(b-c)cos^2(A/2).

Answer 2

Explanation:

1. By the projection rule, we have:

   • $a\cos C + c\cos A = b$ ⇒ $a\cos C = b - c\cos A$,
   • $a\cos B + b\cos A = c$ ⇒ $a\cos B = c - b\cos A$.

2. Subtract the second equation from the first:

   $$a(\cos C - \cos B) = (b - c\cos A) - (c - b\cos A) = (b-c) + (b-c)\cos A.$$

3. Factor out $(b-c)$:

   $$a(\cos C - \cos B) = (b-c)(1+\cos A).$$

4. Recall the half-angle identity:

   $$1+\cos A = 2\cos^2\frac{A}{2}.$$

5. Thus, we obtain:

   $$a(\cos C - \cos B) = 2(b-c)\cos^2\frac{A}{2}.$$

Answer: The identity is proven:

$$a(\cos C - \cos B)=2(b-c)\cos^2\frac{A}{2}.$$

Details:

• Subject: Mathematics
• Chapter: Trigonometry
• Topic: Trigonometric Identities and Projection Rule

Difficulty Level: Easy
Question Type: descriptive