Question

If $|z_1|=2, |z_2|=3, |z_3|=4$ and $|2z_1+3z_2+4z_3|=9$, then value of $|8z_2z_3+27z_3z_1+64z_1z_2|$ is equal to :-

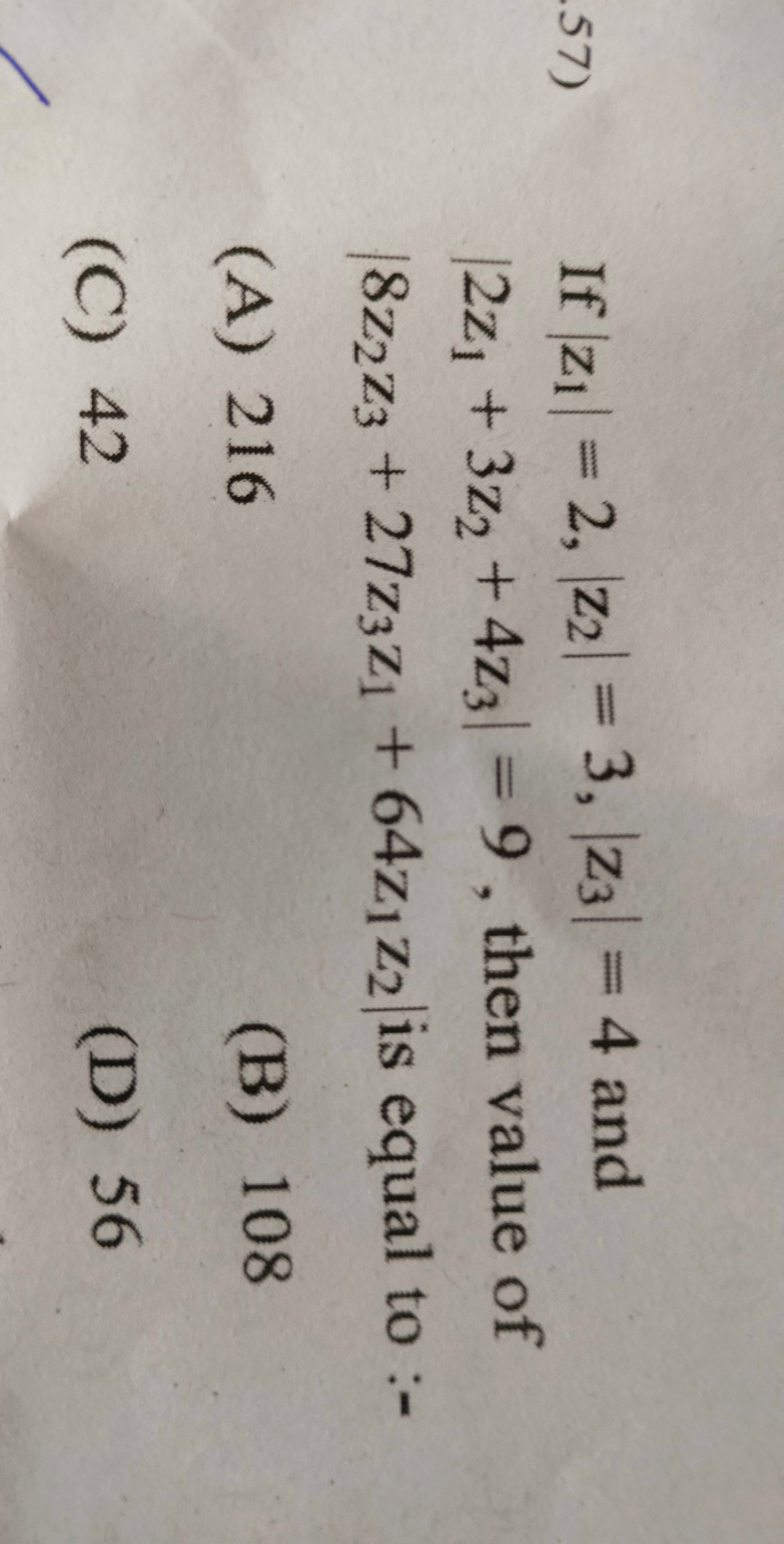
• A. 216
• B. 108
• C. 42
• D. 56

Answer 1

Answer: (A)

216

Answer 2

Solution Explanation:

We are given

$$|z_1|=2,\quad |z_2|=3,\quad |z_3|=4,\quad \text{and} \quad |2z_1+3z_2+4z_3|=9.$$

Notice that the expression to evaluate is

$$8z_2z_3+27z_3z_1+64z_1z_2.$$

Rewrite each term by dividing by $z_1z_2z_3$:

$$\frac{8z_2z_3}{z_1z_2z_3} + \frac{27z_3z_1}{z_1z_2z_3}+\frac{64z_1z_2}{z_1z_2z_3} = \frac{8}{z_1}+\frac{27}{z_2}+\frac{64}{z_3}.$$

Using the property

$$\frac{1}{z}=\frac{\overline{z}}{|z|^2},$$

we get:

$$\frac{8}{z_1}= \frac{8 \overline{z_1}}{4}=2\overline{z_1},\quad \frac{27}{z_2}= \frac{27 \overline{z_2}}{9}=3\overline{z_2},\quad \frac{64}{z_3}= \frac{64 \overline{z_3}}{16}=4\overline{z_3}.$$

Thus,

$$\frac{8z_2z_3+27z_3z_1+64z_1z_2}{z_1z_2z_3} = 2\overline{z_1}+3\overline{z_2}+4\overline{z_3}.$$

Multiplying both sides by $z_1z_2z_3$ gives:

$$8z_2z_3+27z_3z_1+64z_1z_2 = z_1z_2z_3(2\overline{z_1}+3\overline{z_2}+4\overline{z_3}).$$

Taking moduli and using $|z_1z_2z_3| = |z_1||z_2||z_3|$ and $|\,\overline{a}|=|a|$, we have:

$$|8z_2z_3+27z_3z_1+64z_1z_2| = |z_1||z_2||z_3|\,|2z_1+3z_2+4z_3|.$$

Substitute the given values:

$$|z_1||z_2||z_3| = 2\times3\times4 = 24,\quad \text{and}\quad |2z_1+3z_2+4z_3| = 9.$$

Thus,

$$|8z_2z_3+27z_3z_1+64z_1z_2| = 24 \times 9 = 216.$$

Answer: 216 (Option A)