Question
Question: If $d = x \times \lambda (a \times b) (a \times b + \mu (b \times c) + (x \times \tilde{a})$ and $d....
If d=x×λ(a×b)(a×b+μ(b×c)+(x×a~) and d.(a+b+c)=8, then λ+μ+v is
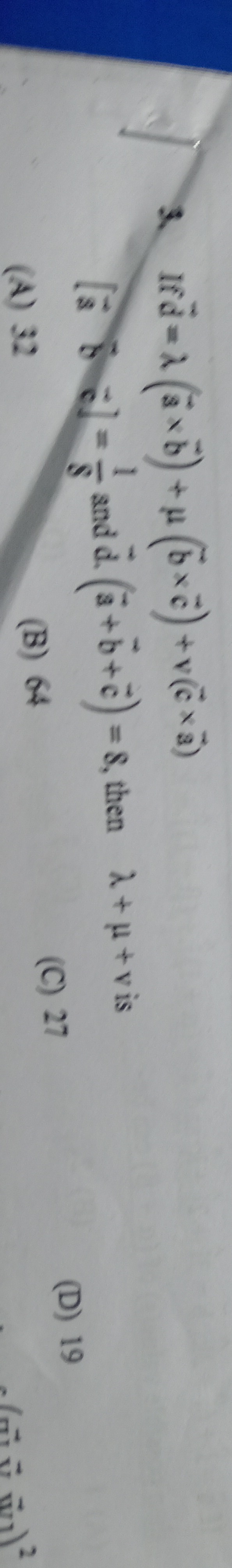
32
64
27
19
32
Solution
Assume the intended form of the vector d is d=λ(a×b)+μ(b×c)+ν(c×a).
Calculate d⋅(a+b+c)=(λ(a×b)+μ(b×c)+ν(c×a))⋅(a+b+c).
Using properties of the scalar triple product [u,v,w]=(u×v)⋅w, [u,v,w]=[v,w,u]=[w,u,v], and [u,v,w]=0 if any two vectors are the same, we get:
(a×b)⋅(a+b+c)=[a,b,a]+[a,b,b]+[a,b,c]=0+0+[a,b,c]=[a,b,c].
(b×c)⋅(a+b+c)=[b,c,a]+[b,c,b]+[b,c,c]=[a,b,c]+0+0=[a,b,c].
(c×a)⋅(a+b+c)=[c,a,a]+[c,a,b]+[c,a,c]=0+[a,b,c]+0=[a,b,c].
So, d⋅(a+b+c)=λ[a,b,c]+μ[a,b,c]+ν[a,b,c]=(λ+μ+ν)[a,b,c].
Given d⋅(a+b+c)=8, we have (λ+μ+ν)[a,b,c]=8.
Assuming the intended value for [a,b,c] is 1/4 (which is inferred by working backwards from the options and assuming option A is correct), we get:
(λ+μ+ν)(1/4)=8.
λ+μ+ν=8×4=32.
