Question

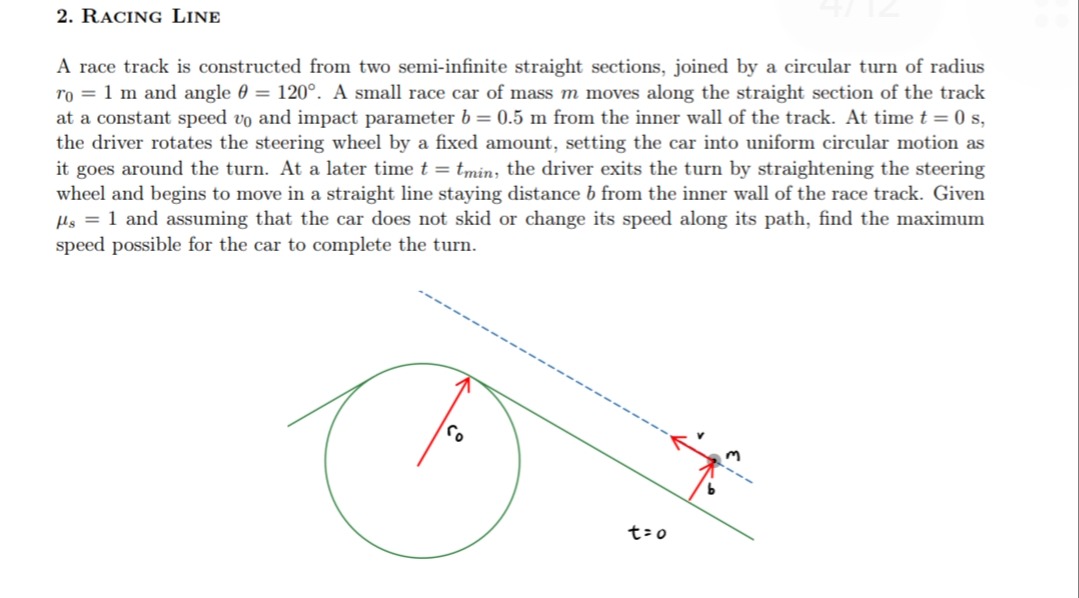
A race track is constructed from two semi-infinite straight sections, joined by a circular turn of radius $r_0$= 1 m and angle $\theta$ = 120°. A small race car of mass $m$ moves along the straight section of the track at a constant speed $v_0$ and impact parameter $b$ = 0.5 m from the inner wall of the track. At time $t$ = 0 s, the driver rotates the steering wheel by a fixed amount, setting the car into uniform circular motion as it goes around the turn. At a later time $t$ = $t_{min}$, the driver exits the turn by straightening the steering wheel and begins to move in a straight line staying distance $b$ from the inner wall of the race track. Given $\mu_s$ = 1 and assuming that the car does not skid or change its speed along its path, find the maximum speed possible for the car to complete the turn.

Answer 1

The maximum speed possible for the car to complete the turn is $\sqrt{15}$ m/s.

Answer 2

The problem asks for the maximum speed a car can have while completing a circular turn without skidding. The centripetal force required for circular motion is provided by the static friction between the tires and the track.

1. Determine the radius of the car's path (R):

   The inner wall of the track has a radius $r_0 = 1$ m. The car maintains a distance $b = 0.5$ m from this inner wall. Therefore, the actual radius of the circular path taken by the car is: $R = r_0 + b = 1 \text{ m} + 0.5 \text{ m} = 1.5 \text{ m}$

2. Identify the forces and conditions for no skidding:

   For the car to move in a circular path, a centripetal force ($F_c$) is required, directed towards the center of the circle. This force is provided by the static friction ($f_s$) between the tires and the road. The centripetal force is given by: $F_c = \frac{mv^2}{R}$

   The maximum static friction available is: $f_{s,max} = \mu_s N$

   Since the track is horizontal, the normal force ($N$) is equal to the car's weight ($mg$): $N = mg$ So, $f_{s,max} = \mu_s mg$

   For the car not to skid, the required centripetal force must be less than or equal to the maximum static friction: $F_c \le f_{s,max}$ $\frac{mv^2}{R} \le \mu_s mg$

3. Calculate the maximum speed ($v_{max}$):

   The maximum speed occurs when the required centripetal force is equal to the maximum static friction: $\frac{mv_{max}^2}{R} = \mu_s mg$ The mass 'm' cancels out from both sides: $\frac{v_{max}^2}{R} = \mu_s g$ $v_{max}^2 = \mu_s g R$ $v_{max} = \sqrt{\mu_s g R}$

4. Substitute the given values:

   Given: $\mu_s = 1$ $R = 1.5 \text{ m}$ Assuming acceleration due to gravity $g = 10 \text{ m/s}^2$ (a common approximation in such problems unless specified otherwise).

   $v_{max} = \sqrt{1 \times 10 \times 1.5}$ $v_{max} = \sqrt{15}$ m/s

The maximum speed possible for the car to complete the turn without skidding is $\sqrt{15}$ m/s. The angle of the turn ($\theta = 120^\circ$) and time ($t_{min}$) are not required to determine the maximum speed.