Question
Question: if $f(x + \frac{1}{x}) = x^2 + \frac{1}{x^2}$ then f(x) = ?...
if f(x+x1)=x2+x21 then f(x) = ?
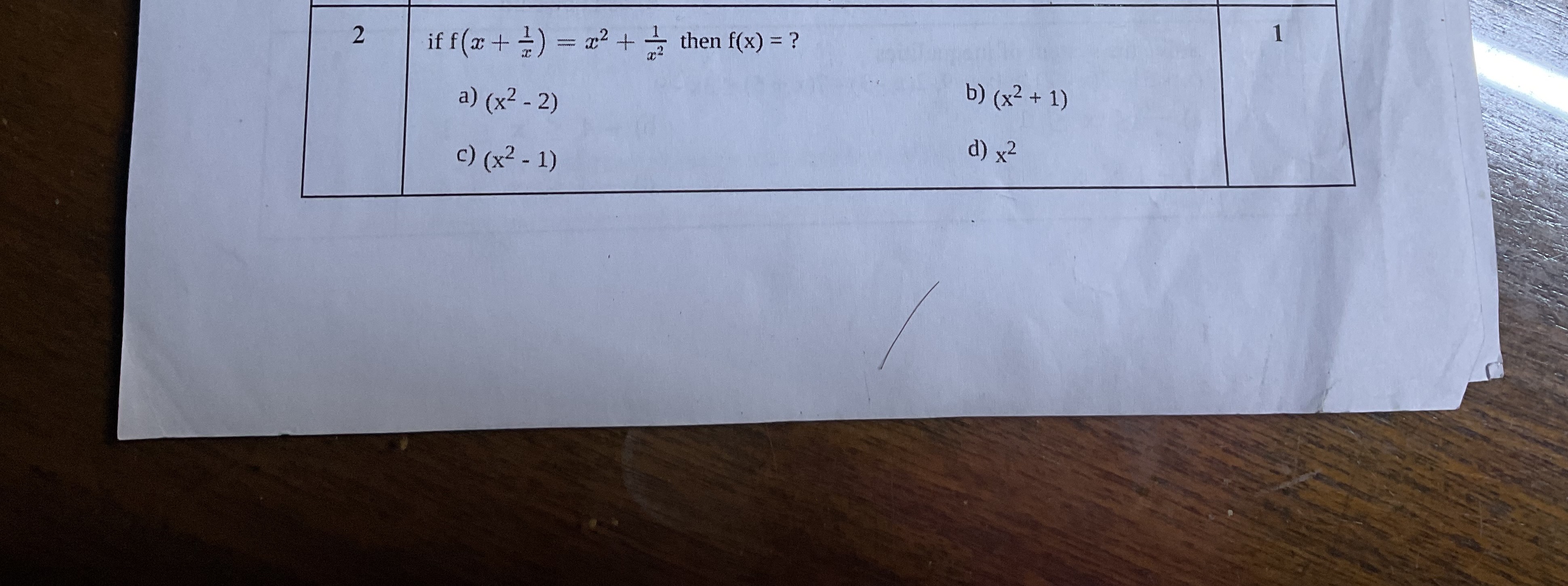
A
(x2−2)
B
(x2+1)
C
(x2−1)
D
x2
Answer
(x2−2)
Explanation
Solution
Let
u=x+x1.
Then
u2=(x+x1)2=x2+2+x21⇒x2+x21=u2−2.
Since the given equation is
f(x+x1)=x2+x21,
we substitute u to obtain:
f(u)=u2−2.
Thus, replacing u by x (as the function variable), we get:
f(x)=x2−2.
