Question
Question: ماهي محصلة كثافة الفيض المغناطيسي عند مركز الحلقة (c)؟...
ماهي محصلة كثافة الفيض المغناطيسي عند مركز الحلقة (c)؟
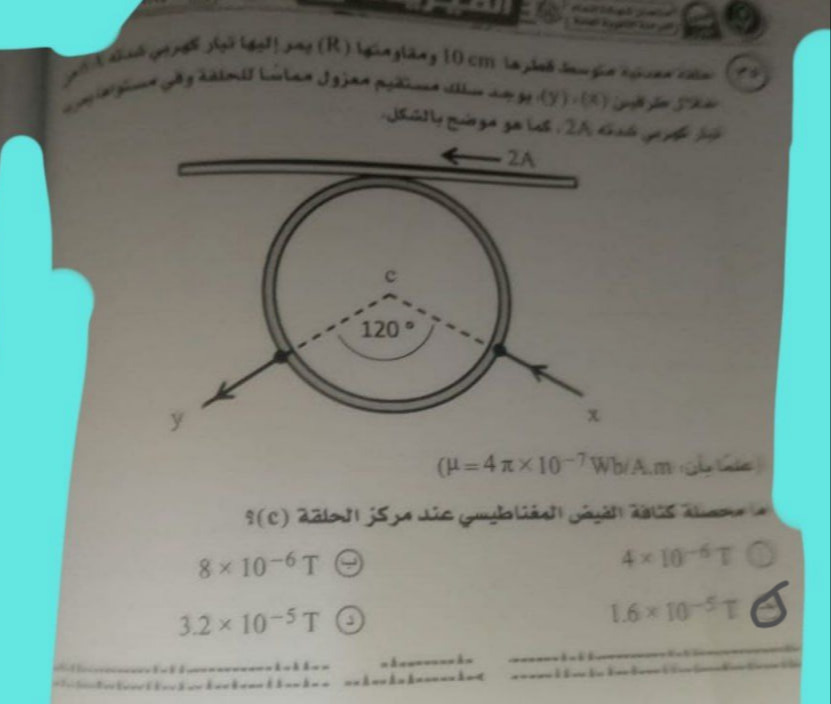
8×10−6T
3.2×10−5T
4×10−6T
1.6×10−5T
8×10−6T
Solution
The problem asks for the net magnetic field at the center (c) of a circular metallic loop. The setup involves two sources of magnetic fields:
- A circular loop with current entering at point x and leaving at point y.
- A straight wire tangent to the loop, carrying a current of 2A.
1. Magnetic field due to the circular loop:
The current I enters the loop at point x and leaves at point y. This means the current divides into two paths: one through the minor arc (between x and y) and another through the major arc (between x and y).
Since the magnetic fields B1 and B2 have equal magnitudes and opposite directions (one into the page, one out of the page), the net magnetic field due to the circular loop at its center is: Bloop=B1−B2=0.
This is a general result: for a current-carrying loop where current enters and leaves at two points, the net magnetic field at the center is always zero.
2. Magnetic field due to the straight wire:
The straight wire is tangent to the top of the loop and carries a current of 2A. The average diameter of the loop is 10 cm, so its radius is r=210 cm=5 cm=0.05 m. Since the wire is tangent to the loop, the perpendicular distance from the center 'c' to the straight wire is equal to the radius of the loop, d=r=0.05 m.
The magnetic field due to a long straight current-carrying wire is given by: Bwire=2πdμ0Iwire Given μ0=4π×10−7 Wb/A.m and Iwire=2 A. Bwire=2π×(0.05 m)(4π×10−7 Wb/A.m)×(2 A)=8×10−6 T.
3. Net magnetic field at center 'c':
The net magnetic field at the center 'c' is the vector sum of the fields due to the loop and the straight wire: Bnet=Bloop+Bwire Since Bloop=0, Bnet=Bwire=8×10−6 T.
