Question

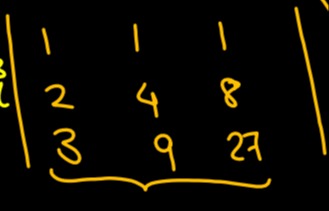
The table shows numbers of the form $n^j$ for $n \in \{1, 2, 3\}$ and $j \in \{1, 2, 3\}$. What is the set-builder form for the set of all unique numbers in the table?

• A. { $x$ | $x = n^j$, $n \in \mathbb{N}$, $1 \le n \le 3$, $j \in \mathbb{N}$, $1 \le j \le 3$ }
• B. { $x$ | $x = n^j$, $n \in \{1, 2, 3\}$, $j \in \{1, 2, 3\}$ }
• C. { $x$ | $x = n^j$, $n \in \mathbb{Z}$, $1 \le n \le 3$, $j \in \mathbb{Z}$, $1 \le j \le 3$ }
• D. { $x$ | $x = n^j$, $n \in \{1, 2, 3\}$, $j \in \{1, 2, 3\}$, $x \in \{1, 2, 3, 4, 8, 9, 27\}$ }

Answer 1

Answer: (A)

{ $x$ | $x = n^j$, $n \in \mathbb{N}$, $1 \le n \le 3$, $j \in \mathbb{N}$, $1 \le j \le 3$ }

Answer 2

The table contains elements generated by raising a row index $n$ to the power of a column index $j$. The row indices are $n=1, 2, 3$, which are natural numbers. The column indices are $j=1, 2, 3$, which are also natural numbers. Therefore, the set of all unique numbers can be represented in set-builder form as $\{ x \mid x = n^j, n \in \mathbb{N}, 1 \le n \le 3, j \in \mathbb{N}, 1 \le j \le 3 \}$.