Question
Question: Train stops at two stations 'd' dist. apert. Time taken = t$\checkmark$ Crux: Never uniform velo a...
Train stops at two stations 'd' dist. apert.
Time taken = t✓ Crux: Never uniform velo
acc = α✓
retar= B✓ Find reln in (α,B,t,d):
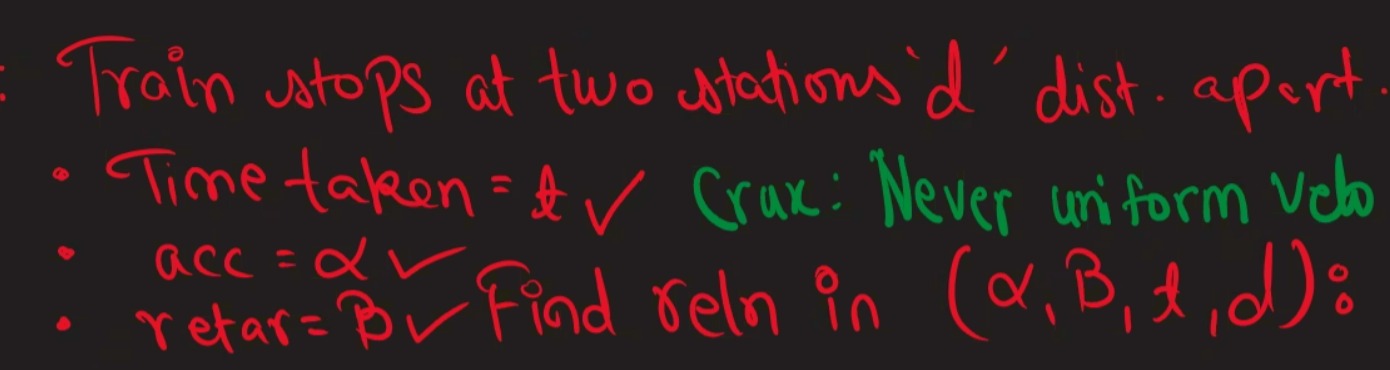
α1+β1=2dt2
Solution
The problem describes a train's motion between two stations, starting from rest and ending at rest. The motion consists of two phases: uniform acceleration and uniform retardation, with no period of constant velocity.
Let:
- d be the total distance between the stations.
- t be the total time taken for the journey.
- α be the acceleration.
- β be the retardation (deceleration).
- vmax be the maximum velocity attained by the train.
- t1 be the time taken during acceleration.
- t2 be the time taken during retardation.
1. Velocity-Time Relationship:
The train starts from rest, accelerates to vmax, and then decelerates to rest. The velocity-time graph for this motion is a triangle.
- During acceleration: vmax=αt1⟹t1=αvmax
- During retardation: 0=vmax−βt2⟹vmax=βt2⟹t2=βvmax
The total time t is the sum of t1 and t2: t=t1+t2=αvmax+βvmax t=vmax(α1+β1) (Equation 1)
2. Distance-Time Relationship:
The total distance d is the area under the velocity-time graph (a triangle). Area = 21×base×height d=21×t×vmax From this, we can express vmax in terms of d and t: vmax=t2d (Equation 2)
3. Combining the Relationships:
Substitute the expression for vmax from Equation 2 into Equation 1: t=(t2d)(α1+β1) Multiply both sides by t: t2=2d(α1+β1) Rearrange the equation to find the desired relation: α1+β1=2dt2
This is the relationship between α, β, t, and d.
Explanation of the solution:
The problem involves two phases of motion: uniform acceleration (α) from rest to maximum velocity (vmax), and uniform retardation (β) from vmax back to rest. The total time is t and total distance is d.
- Express the maximum velocity vmax in terms of acceleration and time (t1) for the first phase, and in terms of retardation and time (t2) for the second phase.
- Sum t1 and t2 to get the total time t in terms of vmax, α, and β.
- Recognize that the velocity-time graph is a triangle. The area under this graph represents the total distance d. Use d=21vmaxt to express vmax in terms of d and t.
- Substitute the expression for vmax from step 3 into the equation from step 2 and simplify to obtain the final relation.
Answer:
The relation between α, β, t, and d is: α1+β1=2dt2
