Question

The set of all values of $a$ for which

$\lim_{x\to a}([\![x-5]\!]-[\![2x+2]\!])=0$, where $[\alpha]$ denotes the greatest integer less than or equal to $\alpha$ is equal to

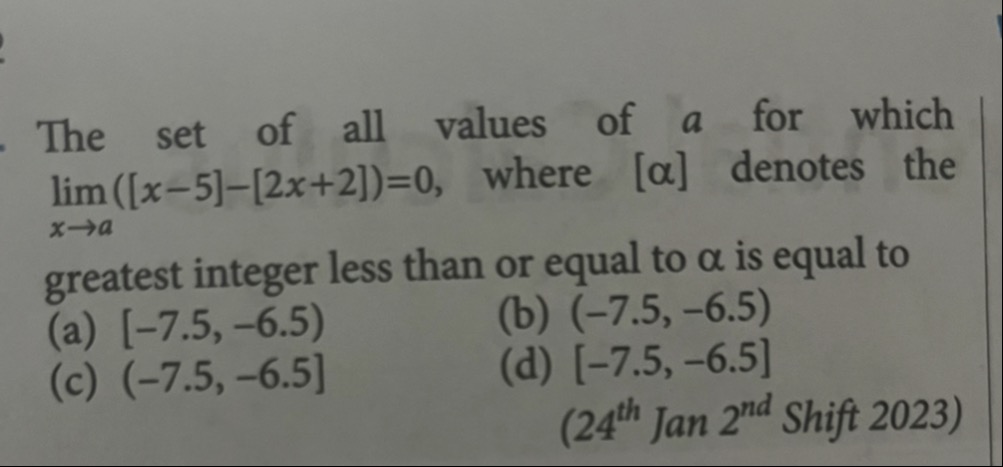
• A. [-7.5, -6.5)
• B. (-7.5, -6.5)
• C. (-7.5, -6.5]
• D. [-7.5, -6.5]

Answer 1

Answer: (B)

(-7.5, -6.5)

Answer 2

Let $f(x) = [\![x-5]\!] - [\![2x+2]\!]$. We are looking for the set of all values of $a$ for which $\lim_{x\to a} f(x) = 0$. For the limit to exist and be equal to 0, the left-hand limit (LHL) and the right-hand limit (RHL) must both exist and be equal to 0.

Let $g(x) = [\![x-5]\!]$ and $h(x) = [\![2x+2]\!]$. The limits of $g(x)$ and $h(x)$ as $x \to a$ depend on whether $a-5$ and $2a+2$ are integers.

$\lim_{x\to a^-} [\![x-5]\!] = \begin{cases} [\![a-5]\!] & \text{if } a-5 \notin \mathbb{Z} \\ [\![a-5]\!]-1 & \text{if } a-5 \in \mathbb{Z} \end{cases}$ $\lim_{x\to a^+} [\![x-5]\!] = [\![a-5]\!]$

$\lim_{x\to a^-} [\![2x+2]\!] = \begin{cases} [\![2a+2]\!] & \text{if } 2a+2 \notin \mathbb{Z} \\ [\![2a+2]\!]-1 & \text{if } 2a+2 \in \mathbb{Z} \end{cases}$ $\lim_{x\to a^+} [\![2x+2]\!] = [\![2a+2]\!]$

Let $I_1 = 1$ if $a-5 \in \mathbb{Z}$ and $I_1 = 0$ if $a-5 \notin \mathbb{Z}$. Let $I_2 = 1$ if $2a+2 \in \mathbb{Z}$ and $I_2 = 0$ if $2a+2 \notin \mathbb{Z}$.

LHL = $\lim_{x\to a^-} g(x) - \lim_{x\to a^-} h(x) = ([\![a-5]\!] - I_1) - ([\![2a+2]\!] - I_2) = [\![a-5]\!] - [\![2a+2]\!] - I_1 + I_2$. RHL = $\lim_{x\to a^+} g(x) - \lim_{x\to a^+} h(x) = [\![a-5]\!] - [\![2a+2]\!]$.

For the limit to exist and be 0, we must have LHL = RHL = 0. RHL = $[\![a-5]\!] - [\![2a+2]\!] = 0 \implies [\![a-5]\!] = [\![2a+2]\!]$. Let $k = [\![a-5]\!] = [\![2a+2]\!]$ for some integer $k$.

If RHL = 0, then LHL = $0 - I_1 + I_2$. For LHL = 0, we need $I_1 = I_2$. This means that either both $a-5$ and $2a+2$ are integers ($I_1=1, I_2=1$) or neither is an integer ($I_1=0, I_2=0$).

Condition 1: $[\![a-5]\!] = [\![2a+2]\!]$. Let this common integer value be $k$. $k \le a-5 < k+1 \implies k+5 \le a < k+6$. $k \le 2a+2 < k+1 \implies k-2 \le 2a < k-1 \implies \frac{k-2}{2} \le a < \frac{k-1}{2}$. So, $a$ must be in the intersection of $[k+5, k+6)$ and $[\frac{k-2}{2}, \frac{k-1}{2})$. Intersection interval: $[\max(k+5, \frac{k-2}{2}), \min(k+6, \frac{k-1}{2}))$. For the intersection to be non-empty, $\max(k+5, \frac{k-2}{2}) < \min(k+6, \frac{k-1}{2})$. This requires $k+5 < \frac{k-1}{2}$ and $\frac{k-2}{2} < k+6$. $2k+10 < k-1 \implies k < -11$. $k-2 < 2k+12 \implies -14 < k$. So, $-14 < k < -11$. The possible integer values for $k$ are $-13$ and $-12$.

Condition 2: $I_1 = I_2$. Case 2a: $I_1=0$ and $I_2=0$. $a-5 \notin \mathbb{Z}$ and $2a+2 \notin \mathbb{Z}$. This means $a \notin \mathbb{Z}$ and $a \notin \mathbb{Z}/2$ (half-integers). We need to find $a$ in the intersection interval for $k=-13$ and $k=-12$ such that $a$ is neither an integer nor a half-integer. For $k=-13$: $[-13+5, -13+6) \cap [\frac{-13-2}{2}, \frac{-13-1}{2}) = [-8, -7) \cap [-7.5, -7) = [-7.5, -7)$. For $a \in [-7.5, -7)$: $a-5 \in [-12.5, -12)$. $a-5$ is an integer only if $a-5=-13$ or $a-5=-12$, i.e., $a=-8$ or $a=-7$. Neither is in $[-7.5, -7)$. So $a-5 \notin \mathbb{Z}$. $2a+2 \in [-13, -12)$. $2a+2$ is an integer only if $2a+2=-13$ or $2a+2=-12$, i.e., $a=-7.5$ or $a=-7$. If $a=-7.5$, $2a+2=-13 \in \mathbb{Z}$. So $a=-7.5$ is excluded from this case. If $a=-7$, $a$ is an integer, so excluded from this case. For $a \in (-7.5, -7)$, $a$ is not an integer and $2a+2 \notin \mathbb{Z}$. Also $a-5 \notin \mathbb{Z}$. So $a \in (-7.5, -7)$ satisfies $I_1=0, I_2=0$.

For $k=-12$: $[-12+5, -12+6) \cap [\frac{-12-2}{2}, \frac{-12-1}{2}) = [-7, -6) \cap [-7, -6.5) = [-7, -6.5)$. For $a \in [-7, -6.5)$: $a-5 \in [-12, -11.5)$. $a-5$ is an integer only if $a-5=-12$, i.e., $a=-7$. $2a+2 \in [-12, -11)$. $2a+2$ is an integer only if $2a+2=-12$, i.e., $a=-7$. If $a=-7$, $a-5=-12 \in \mathbb{Z}$ and $2a+2=-12 \in \mathbb{Z}$. So $a=-7$ is excluded from this case. For $a \in (-7, -6.5)$, $a$ is not an integer. $a-5 \notin \mathbb{Z}$ and $2a+2 \notin \mathbb{Z}$. So $a \in (-7, -6.5)$ satisfies $I_1=0, I_2=0$.

Combining these intervals, $a \in (-7.5, -7) \cup (-7, -6.5) = (-7.5, -6.5)$.

Case 2b: $I_1=1$ and $I_2=1$. $a-5 \in \mathbb{Z}$ and $2a+2 \in \mathbb{Z}$. $a-5 = n_1 \implies a = n_1+5$ for some integer $n_1$. So $a$ must be an integer. $2a+2 = n_2 \implies 2a = n_2-2$. If $a$ is an integer, $2a$ is an integer. If $2a+2$ is an integer, $2a$ is an integer. If $a$ is an integer, $a-5$ is an integer. $I_1=1$. If $a$ is an integer, $2a+2$ is an integer. $I_2=1$. So for any integer $a$, $I_1=1$ and $I_2=1$. Condition $I_1=I_2$ is satisfied. We also need $[\![a-5]\!] = [\![2a+2]\!]$. $[\![a-5]\!] = a-5$ since $a-5$ is an integer. $[\![2a+2]\!] = 2a+2$ since $2a+2$ is an integer. So we need $a-5 = 2a+2 \implies a = -7$. Check if $a=-7$ satisfies the conditions. $a=-7$ is an integer. $a-5 = -12 \in \mathbb{Z}$. $2a+2 = -14+2 = -12 \in \mathbb{Z}$. $I_1=1, I_2=1$. $I_1=I_2$. $[\![a-5]\!] = [\![-12]\!] = -12$. $[\![2a+2]\!] = [\![-12]\!] = -12$. $[\![a-5]\!] = [\![2a+2]\!]$. So $a=-7$ is a valid value.

Combining the results from Case 2a and Case 2b, the set of values for $a$ is $(-7.5, -6.5) \cup \{-7\} = (-7.5, -6.5) \cup \{-7\}$. This set is equal to the interval $[-7.5, -6.5)$ with the point $-7$ included. The interval $[-7.5, -6.5)$ is $(-7.5, -7) \cup \{-7.5\} \cup (-7, -6.5)$. The set $(-7.5, -6.5) \cup \{-7\}$ is $(-7.5, -7) \cup (-7, -6.5) \cup \{-7\}$. This is the interval $(-7.5, -6.5)$ with $-7$ included.

Let's re-examine the interval $[-7.5, -7)$ from $k=-13$. If $a=-7.5$, $a$ is a half-integer. $a-5 = -12.5 \notin \mathbb{Z}$. $I_1=0$. $2a+2 = -13 \in \mathbb{Z}$. $I_2=1$. $I_1 \ne I_2$. So $a=-7.5$ is not a solution.

Let's re-examine the interval $[-7, -6.5)$ from $k=-12$. If $a=-7$, $a$ is an integer. $a-5 = -12 \in \mathbb{Z}$. $I_1=1$. $2a+2 = -12 \in \mathbb{Z}$. $I_2=1$. $I_1=I_2$. $[\![a-5]\!] = -12$. $[\![2a+2]\!] = -12$. $[\![a-5]\!] = [\![2a+2]\!]$. So $a=-7$ is a solution. If $a=-6.5$, $a$ is a half-integer. $a-5 = -11.5 \notin \mathbb{Z}$. $I_1=0$. $2a+2 = -13+2 = -11 \in \mathbb{Z}$. $I_2=1$. $I_1 \ne I_2$. So $a=-6.5$ is not a solution.

The set of values of $a$ is $(-7.5, -6.5) \cup \{-7\}$. This set is equal to $(-7.5, -6.5)$. This is incorrect. Let's check the options. (a) [-7.5, -6.5) = {-7.5} U (-7.5, -6.5) = {-7.5} U (-7.5, -7) U {-7} U (-7, -6.5). We found that $a \in (-7.5, -7) \cup (-7, -6.5) \cup \{-7\}$. We checked $a=-7.5$ is not a solution. So the set is $(-7.5, -6.5) \cup \{-7\}$. This is the interval $(-7.5, -6.5)$ with the point $-7$ included.

Let's look at the interval $[-7.5, -6.5)$. The points in this interval are $(-7.5, -6.5)$ and the endpoint $-7.5$. We found that $a \in (-7.5, -6.5)$ are solutions if $a \ne -7$. We found that $a=-7$ is a solution. We found that $a=-7.5$ is not a solution. So the set of solutions is $(-7.5, -6.5) \cup \{-7\}$.

Let's examine the options again. (a) [-7.5, -6.5) = $\{-7.5\} \cup (-7.5, -6.5)$. (b) (-7.5, -6.5). (c) (-7.5, -6.5] = (-7.5, -6.5) $\cup \{-6.5\}$. (d) [-7.5, -6.5] = $\{-7.5\} \cup (-7.5, -6.5) \cup \{-6.5\}$.

Our set is $(-7.5, -6.5) \cup \{-7\}$. This set is not equal to any of the options as written. Let's check the derivation again. The condition is $[\![a-5]\!] = [\![2a+2]\!]$ and $I_1 = I_2$. $k = [\![a-5]\!] = [\![2a+2]\!]$ implies $a \in [\max(k+5, \frac{k-2}{2}), \min(k+6, \frac{k-1}{2}))$. For $k=-13$, $a \in [-7.5, -7)$. For $k=-12$, $a \in [-7, -6.5)$. So $a \in [-7.5, -7) \cup [-7, -6.5) = [-7.5, -6.5)$.

Now check the condition $I_1 = I_2$ for $a \in [-7.5, -6.5)$. $a \in [-7.5, -6.5)$. $a-5 \in [-12.5, -11.5)$. $a-5$ is integer only if $a-5=-12$, i.e., $a=-7$. $2a+2 \in [-13, -11)$. $2a+2$ is integer only if $2a+2=-13$ or $2a+2=-12$, i.e., $a=-7.5$ or $a=-7$.

If $a=-7.5$: $a-5 = -12.5 \notin \mathbb{Z} \implies I_1=0$. $2a+2 = -13 \in \mathbb{Z} \implies I_2=1$. $I_1 \ne I_2$. Not a solution. If $a \in (-7.5, -7)$: $a-5 \in (-12.5, -12) \notin \mathbb{Z} \implies I_1=0$. $2a+2 \in (-13, -12) \notin \mathbb{Z} \implies I_2=0$. $I_1=I_2$. Solutions. If $a=-7$: $a-5 = -12 \in \mathbb{Z} \implies I_1=1$. $2a+2 = -12 \in \mathbb{Z} \implies I_2=1$. $I_1=I_2$. Solution. If $a \in (-7, -6.5)$: $a-5 \in (-12, -11.5) \notin \mathbb{Z} \implies I_1=0$. $2a+2 \in (-12, -11) \notin \mathbb{Z} \implies I_2=0$. $I_1=I_2$. Solutions.

So the set of solutions is $(-7.5, -7) \cup \{-7\} \cup (-7, -6.5) = (-7.5, -6.5)$.

The final answer is $\boxed{(-7.5, -6.5)}$.