Question

Determine the domain and range of the function $f(x) = - \sqrt{x^3-1}$.

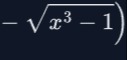
• A. Domain: $[1, \infty)$, Range: $(-\infty, 0]$
• B. Domain: $(-\infty, 1]$, Range: $[0, \infty)$
• C. Domain: $(-\infty, \infty)$, Range: $(-\infty, \infty)$
• D. Domain: $[0, \infty)$, Range: $(-\infty, 0]$

Answer 1

Answer: (A)

Domain: $[1, \infty)$, Range: $(-\infty, 0]$

Answer 2

To determine the domain, we need to ensure that the expression under the square root is non-negative: $x^3 - 1 \ge 0$ $x^3 \ge 1$ Taking the cube root of both sides gives: $x \ge 1$ So, the domain is $[1, \infty)$.

To determine the range, let $y = - \sqrt{x^3-1}$. Since $\sqrt{x^3-1} \ge 0$ for $x \ge 1$, multiplying by $-1$ means that $-\sqrt{x^3-1} \le 0$. Thus, $y \le 0$. At the lower bound of the domain, $x=1$: $f(1) = - \sqrt{1^3 - 1} = - \sqrt{0} = 0$ As $x$ approaches infinity, $x^3-1$ approaches infinity, so $-\sqrt{x^3-1}$ approaches $-\infty$. Therefore, the range is $(-\infty, 0]$.