Question
Question: A dipole is formed by two point charge -q and +q, each of mass m, and both are connected by a rod of...
A dipole is formed by two point charge -q and +q, each of mass m, and both are connected by a rod of length l and mass m. This dipole is placed in uniform. If the dipole is disturbed by a small angle θ from stable equilibrium position motion will be almost SHM. Also find its time period. If the dipole is disturbed by θ angle, τnet = -PE sinθ (Here -ve sign indicates torque is opposite to θ)
If θ is very small, sinθ ≈ θ ∴ τnet = - (PE)θ τnet ∝ (-θ) so motion will be almost SHM & C = PE (where, P = ql)
∴ T=2π CI
∴ T = 2mPE12ml+2m(2l)2 = 2π qlE12ml+2ml2 = 2π 12qlE7ml2 = 2π 12qE7ml
T = π 3qE7ml
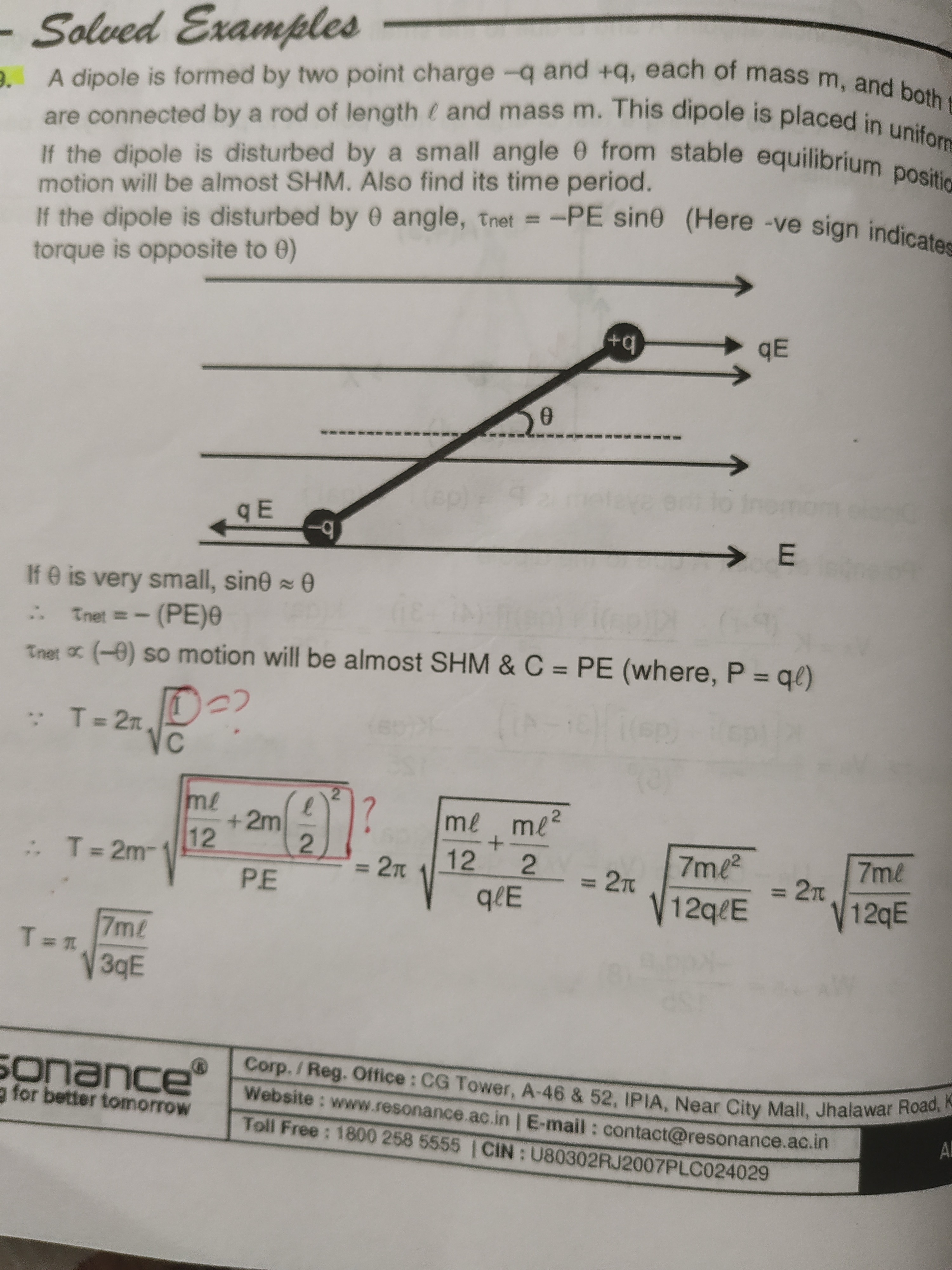
T = π 3qE7ml
Solution
Explanation of the Solution:
-
Torque on the Dipole: When an electric dipole with dipole moment p is placed in a uniform electric field E, it experiences a torque given by τ=p×E. The magnitude of this torque is τ=pEsinθ, where θ is the angle between p and E. For a dipole formed by charges +q and -q separated by length l, the dipole moment is p=ql. The stable equilibrium position is when the dipole moment is aligned with the electric field (θ=0∘). If the dipole is disturbed by a small angle θ from this position, the torque acts as a restoring torque, trying to bring it back to equilibrium. Therefore, we write τnet=−pEsinθ. The negative sign indicates that the torque is opposite to the angular displacement.
-
Small Angle Approximation for SHM: For small angular displacements, sinθ≈θ (in radians). Substituting this into the torque equation, we get τnet=−pEθ. This equation is in the form of angular Simple Harmonic Motion (SHM), τnet=−Cθ, where C is the torsional constant. By comparison, C=pE=qlE. Since the restoring torque is directly proportional to the negative of the angular displacement, the motion will be approximately SHM for small angles.
-
Moment of Inertia (I): The system consists of a rod of mass m and length l, and two point charges, each of mass m, attached at the ends of the rod. The rotation occurs about the center of mass of the system, which is the midpoint of the rod.
- Moment of inertia of the rod about its center: Irod=121ml2.
- Moment of inertia of each point charge about the center of the rod: Icharge=mr2. Here, r=l/2 (distance from the center to each charge). So, for one charge, Icharge=m(l/2)2=41ml2.
- Total moment of inertia of the two charges: I2charges=2×41ml2=21ml2.
- Total moment of inertia of the dipole system: I=Irod+I2charges=121ml2+21ml2 To add these, find a common denominator (12): I=12ml2+126ml2=127ml2.
-
Time Period of SHM: The time period for angular SHM is given by the formula T=2πCI. Substitute the calculated values of I and C: T=2πqlE127ml2 T=2π12qlE7ml2 Cancel one 'l' from the numerator and denominator: T=2π12qE7ml To simplify further, move the '2' inside the square root by squaring it (2=4): T=π4×12qE7ml T=π12qE28ml Divide both 28 and 12 by their greatest common divisor, which is 4: T=π3qE7ml
The final expression for the time period of oscillation is T=π3qE7ml.
