Question

Let $\lambda \in Z$, $\vec{a} = \lambda \hat{i} + \hat{j} - \hat{k}$ and $\vec{b} = 3\hat{i} - \hat{j} + 2\hat{k}$. Let $\vec{c}$ be a vector such that $(\vec{a} + \vec{b} + \vec{c}) \times \vec{c} = \vec{0}, \vec{a} \cdot \vec{c} = -17$ and $\vec{b} \cdot \vec{c} = -20$. Then $|\vec{c} \times (\lambda \hat{i} + \hat{j} + \hat{k})|^{2}$ is equal to :

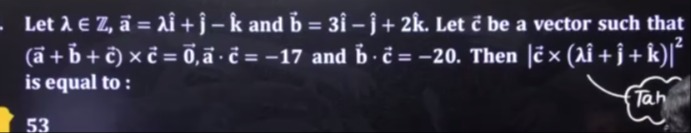
Answer 1

46

Answer 2

The condition $(\vec{a} + \vec{b} + \vec{c}) \times \vec{c} = \vec{0}$ implies that $\vec{a} + \vec{b}$ is parallel to $\vec{c}$. Thus, $\vec{c} = k(\vec{a} + \vec{b})$ for some scalar $k$. $\vec{a} + \vec{b} = (\lambda+3)\hat{i} + \hat{k}$. So, $\vec{c} = k((\lambda+3)\hat{i} + \hat{k})$. Using the given dot product conditions, $\vec{a} \cdot \vec{c} = -17$ and $\vec{b} \cdot \vec{c} = -20$, we get: $k(\lambda^2 + 3\lambda - 1) = -17$ $k(3\lambda + 11) = -20$ Equating the expressions for $k$ gives $20\lambda^2 + 9\lambda - 207 = 0$. The integer solution is $\lambda = 3$. Substituting $\lambda = 3$ into $k(3\lambda + 11) = -20$ gives $k = -1$. With $\lambda = 3$ and $k = -1$, we find $\vec{c} = -6\hat{i} - \hat{k}$ and $\vec{u} = 3\hat{i} + \hat{j} + \hat{k}$. The cross product $\vec{c} \times \vec{u} = \hat{i} + 3\hat{j} - 6\hat{k}$. The magnitude squared is $|\vec{c} \times \vec{u}|^2 = 1^2 + 3^2 + (-6)^2 = 1 + 9 + 36 = 46$.