Question

• Find number of moles and total number of atoms present in ⅰ) 18 g H₂O(s) ii) 18 ml H₂O(v) (ii) 18 ml H₂O(l)

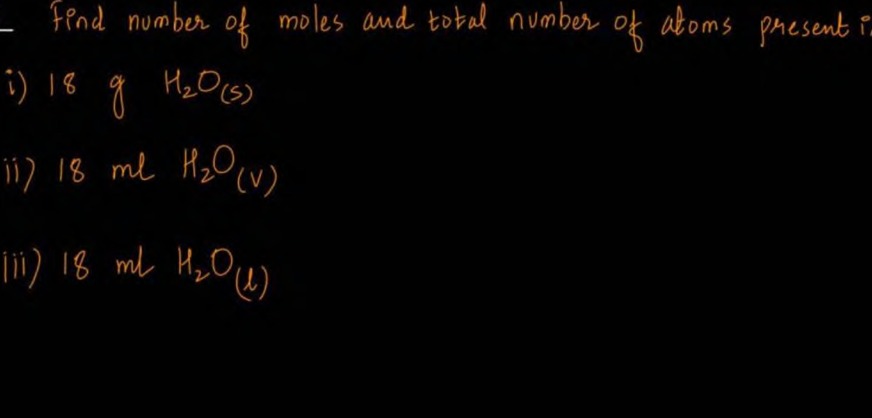
Answer 1

ⅰ) 18 g H₂O(s)

• Number of moles: 1 mole
• Total number of atoms: $1.8066 \times 10^{24}$ atoms

ii) 18 ml H₂O(v) (Assuming STP)

• Number of moles: 0.00080357 moles
• Total number of atoms: $1.452 \times 10^{21}$ atoms

iii) 18 ml H₂O(l)

• Number of moles: 1 mole
• Total number of atoms: $1.8066 \times 10^{24}$ atoms

Answer 2

The problem asks to calculate the number of moles and total number of atoms present in water in different states and given quantities.

Key Concepts and Formulas Used:

1. Molar Mass (M): The mass of one mole of a substance. For H₂O, M = (2 × Atomic mass of H) + (1 × Atomic mass of O) = (2 × 1.008) + (1 × 16.00) ≈ 18 g/mol.
2. Number of Moles (n):
   • If mass (m) is given: $n = \frac{\text{Mass}}{\text{Molar Mass}} = \frac{m}{M}$
   • If volume (V) of a gas at STP is given: $n = \frac{\text{Volume}}{\text{Molar Volume at STP}} = \frac{V}{22.4 \text{ L/mol}}$ (or 22400 mL/mol)
3. Avogadro's Number (N_A): The number of particles (atoms, molecules, ions, etc.) in one mole of a substance, which is approximately $6.022 \times 10^{23} \text{ particles/mol}$.
4. Number of Molecules: Number of moles × Avogadro's Number ($N = n \times N_A$)
5. Total Number of Atoms: Number of molecules × Number of atoms per molecule.
   • For H₂O, there are 2 Hydrogen atoms and 1 Oxygen atom, so 3 atoms per molecule.
6. Density (ρ): $\rho = \frac{\text{Mass}}{\text{Volume}}$. This is used to convert volume to mass for liquids/solids.
   • Density of liquid water (H₂O(l)) is approximately $1 \text{ g/mL}$.

---

Calculations:

ⅰ) 18 g H₂O(s)

• Mass of H₂O(s): $m = 18 \text{ g}$
• Molar Mass of H₂O: $M = 18 \text{ g/mol}$
• Number of Moles: $n = \frac{m}{M} = \frac{18 \text{ g}}{18 \text{ g/mol}} = 1 \text{ mol}$
• Number of Molecules: $N = n \times N_A = 1 \text{ mol} \times 6.022 \times 10^{23} \text{ molecules/mol} = 6.022 \times 10^{23} \text{ molecules}$
• Total Number of Atoms: (Each H₂O molecule has 3 atoms: 2 H + 1 O) Total atoms = $N \times 3 = 6.022 \times 10^{23} \times 3 = 1.8066 \times 10^{24} \text{ atoms}$

ii) 18 ml H₂O(v)

• Assumption: Water vapor (H₂O(v)) is a gas. Since no temperature or pressure is given, we assume Standard Temperature and Pressure (STP), where T = 0°C (273.15 K) and P = 1 atm. At STP, the molar volume of any ideal gas is $22.4 \text{ L/mol}$ or $22400 \text{ mL/mol}$.
• Volume of H₂O(v): $V = 18 \text{ mL}$
• Number of Moles: $n = \frac{V}{\text{Molar Volume at STP}} = \frac{18 \text{ mL}}{22400 \text{ mL/mol}} \approx 0.00080357 \text{ mol}$
• Number of Molecules: $N = n \times N_A = 0.00080357 \text{ mol} \times 6.022 \times 10^{23} \text{ molecules/mol} \approx 4.840 \times 10^{20} \text{ molecules}$
• Total Number of Atoms: (Each H₂O molecule has 3 atoms) Total atoms = $N \times 3 = 4.840 \times 10^{20} \times 3 \approx 1.452 \times 10^{21} \text{ atoms}$

iii) 18 ml H₂O(l)

• Assumption: The density of liquid water (H₂O(l)) is approximately $1 \text{ g/mL}$.
• Volume of H₂O(l): $V = 18 \text{ mL}$
• Mass of H₂O(l): $m = \rho \times V = 1 \text{ g/mL} \times 18 \text{ mL} = 18 \text{ g}$
• Molar Mass of H₂O: $M = 18 \text{ g/mol}$
• Number of Moles: $n = \frac{m}{M} = \frac{18 \text{ g}}{18 \text{ g/mol}} = 1 \text{ mol}$
• Number of Molecules: $N = n \times N_A = 1 \text{ mol} \times 6.022 \times 10^{23} \text{ molecules/mol} = 6.022 \times 10^{23} \text{ molecules}$
• Total Number of Atoms: (Each H₂O molecule has 3 atoms) Total atoms = $N \times 3 = 6.022 \times 10^{23} \times 3 = 1.8066 \times 10^{24} \text{ atoms}$

---

Explanation of the solution:

1. For 18 g H₂O(s): Calculate moles by dividing given mass by molar mass of H₂O (18 g/mol). Then multiply moles by Avogadro's number to get molecules, and by 3 (atoms per H₂O molecule) for total atoms.
2. For 18 ml H₂O(v): Assume STP conditions (0°C, 1 atm) where 1 mole of gas occupies 22.4 L (22400 mL). Calculate moles by dividing the given volume by molar volume at STP. Then proceed as above to find molecules and total atoms.
3. For 18 ml H₂O(l): Assume density of liquid water is 1 g/mL. Convert volume to mass using density. Then proceed as in part (i) to find moles, molecules, and total atoms.