Question

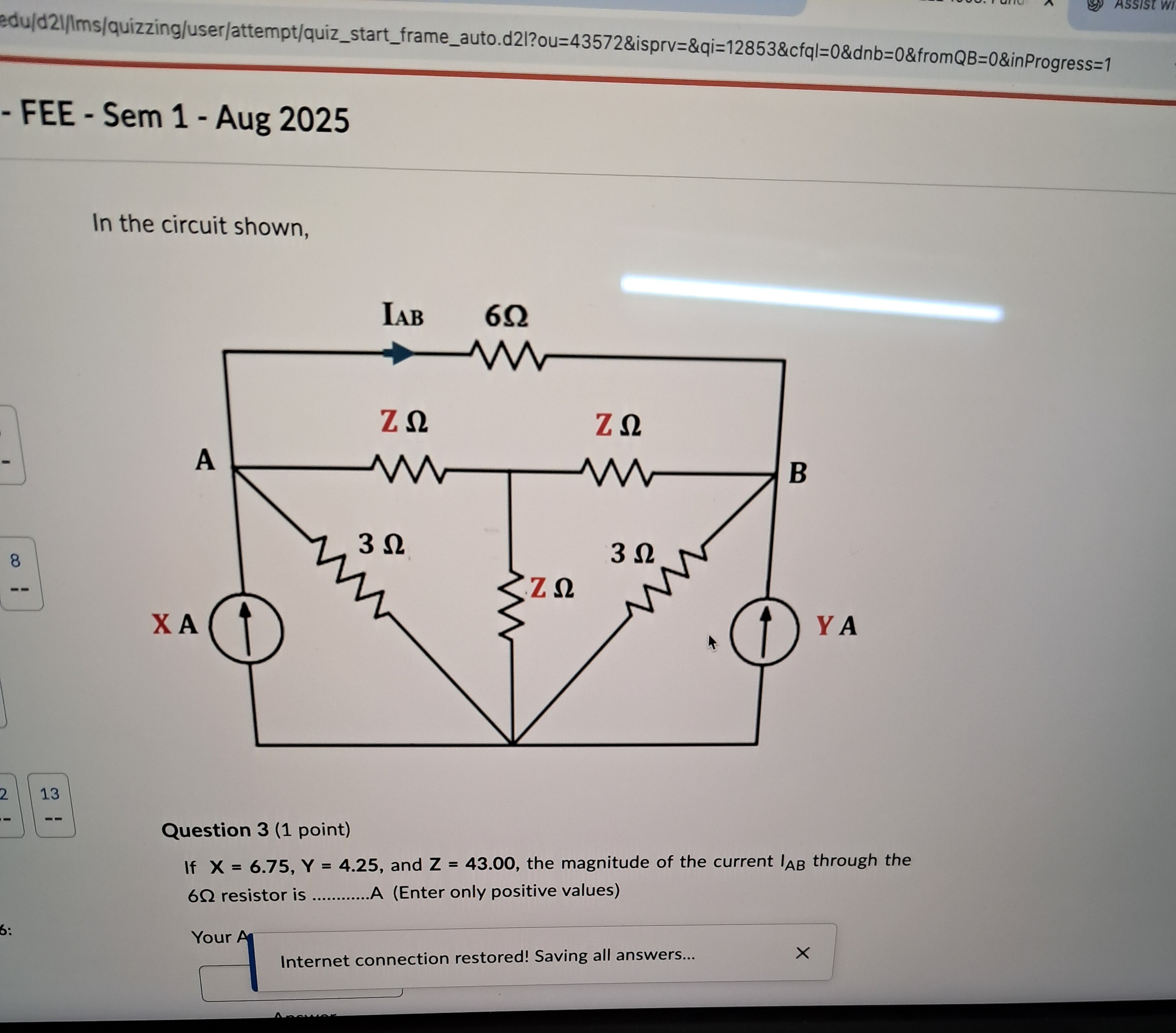
In the circuit shown,

If X = 6.75, Y = 4.25, and Z = 43.00, the magnitude of the current $I_{AB}$ through the 6Ω resistor is .................A (Enter only positive values)

Answer 1

0.60

Answer 2

To solve this problem, we will use nodal analysis. Let the potential at the bottom common line (Node D) be the reference node, so $V_D = 0$ V. Let the potentials at nodes A, B, and C be $V_A$, $V_B$, and $V_C$ respectively.

The given values are: X = 6.75 A Y = 4.25 A Z = 43.00 Ω

1. Kirchhoff's Current Law (KCL) at Node A:
The current X enters node A. The currents leaving node A are through the 6Ω resistor (to B), the ZΩ resistor (to C), and the 3Ω resistor (to D). $X = \frac{V_A - V_B}{6} + \frac{V_A - V_C}{Z} + \frac{V_A - V_D}{3}$
Since $V_D = 0$:
$6.75 = \frac{V_A - V_B}{6} + \frac{V_A - V_C}{43} + \frac{V_A}{3}$
To eliminate denominators, multiply the entire equation by $LCM(6, 43, 3) = 258$:
$6.75 \times 258 = 43(V_A - V_B) + 6(V_A - V_C) + 86V_A$
$1741.5 = 43V_A - 43V_B + 6V_A - 6V_C + 86V_A$
$1741.5 = (43 + 6 + 86)V_A - 43V_B - 6V_C$
$1741.5 = 135V_A - 43V_B - 6V_C$ (Equation 1)

2. KCL at Node B:
The current Y enters node B. The currents leaving node B are through the 6Ω resistor (to A), the ZΩ resistor (to C), and the 3Ω resistor (to D). $Y = \frac{V_B - V_A}{6} + \frac{V_B - V_C}{Z} + \frac{V_B - V_D}{3}$
Since $V_D = 0$:
$4.25 = \frac{V_B - V_A}{6} + \frac{V_B - V_C}{43} + \frac{V_B}{3}$
Multiply by 258:
$4.25 \times 258 = 43(V_B - V_A) + 6(V_B - V_C) + 86V_B$
$1096.5 = 43V_B - 43V_A + 6V_B - 6V_C + 86V_B$
$1096.5 = -43V_A + (43 + 6 + 86)V_B - 6V_C$
$1096.5 = -43V_A + 135V_B - 6V_C$ (Equation 2)

3. KCL at Node C:
There are no current sources connected to node C. The sum of currents leaving node C must be zero. The currents leave through the ZΩ resistors to A, B, and D. $\frac{V_C - V_A}{Z} + \frac{V_C - V_B}{Z} + \frac{V_C - V_D}{Z} = 0$
Since $V_D = 0$:
$\frac{V_C - V_A}{43} + \frac{V_C - V_B}{43} + \frac{V_C}{43} = 0$
Multiply by 43:
$(V_C - V_A) + (V_C - V_B) + V_C = 0$
$3V_C - V_A - V_B = 0$
$V_A + V_B = 3V_C$ (Equation 3)

Now we have a system of three linear equations:

1. $135V_A - 43V_B - 6V_C = 1741.5$
2. $-43V_A + 135V_B - 6V_C = 1096.5$
3. $V_A + V_B = 3V_C \implies V_C = \frac{V_A + V_B}{3}$

Substitute $V_C$ from Equation 3 into Equation 1:
$135V_A - 43V_B - 6\left(\frac{V_A + V_B}{3}\right) = 1741.5$
$135V_A - 43V_B - 2(V_A + V_B) = 1741.5$
$135V_A - 43V_B - 2V_A - 2V_B = 1741.5$
$(135 - 2)V_A - (43 + 2)V_B = 1741.5$
$133V_A - 45V_B = 1741.5$ (Equation 4)

Substitute $V_C$ from Equation 3 into Equation 2:
$-43V_A + 135V_B - 6\left(\frac{V_A + V_B}{3}\right) = 1096.5$
$-43V_A + 135V_B - 2(V_A + V_B) = 1096.5$
$-43V_A + 135V_B - 2V_A - 2V_B = 1096.5$
$(-43 - 2)V_A + (135 - 2)V_B = 1096.5$
$-45V_A + 133V_B = 1096.5$ (Equation 5)

Now we have a system of two equations with two unknowns ($V_A, V_B$): 4. $133V_A - 45V_B = 1741.5$ 5. $-45V_A + 133V_B = 1096.5$

We need to find the current $I_{AB}$ through the 6Ω resistor, which is given by $I_{AB} = \frac{V_A - V_B}{6}$.
To find $(V_A - V_B)$, subtract Equation 5 from Equation 4:
$(133V_A - 45V_B) - (-45V_A + 133V_B) = 1741.5 - 1096.5$
$133V_A - 45V_B + 45V_A - 133V_B = 645$
$(133 + 45)V_A - (45 + 133)V_B = 645$
$178V_A - 178V_B = 645$
$178(V_A - V_B) = 645$
$V_A - V_B = \frac{645}{178}$

Now, calculate $I_{AB}$:
$I_{AB} = \frac{1}{6} \times (V_A - V_B)$
$I_{AB} = \frac{1}{6} \times \frac{645}{178}$
$I_{AB} = \frac{645}{1068}$

Calculate the numerical value:
$I_{AB} \approx 0.6039325842696629$ A

Rounding to two decimal places, as consistent with the input values:
$I_{AB} \approx 0.60$ A

The question asks for the magnitude and to enter only positive values. Our result is positive.

The final answer is $\boxed{\text{0.60}}$.

Explanation of the solution:

1. Define node voltages ($V_A, V_B, V_C, V_D$) and set $V_D = 0$ V (ground).
2. Apply Kirchhoff's Current Law (KCL) at nodes A, B, and C to form a system of linear equations.
   • KCL at A: Sum of currents leaving A equals current entering A (X).
   • KCL at B: Sum of currents leaving B equals current entering B (Y).
   • KCL at C: Sum of currents leaving C equals zero (no current sources).
3. Simplify the equations by substituting the given values of X, Y, and Z.
4. Solve the system of equations. From KCL at C, express $V_C$ in terms of $V_A$ and $V_B$.
5. Substitute the expression for $V_C$ into the KCL equations for A and B, reducing the system to two equations with two unknowns ($V_A, V_B$).
6. Solve for $(V_A - V_B)$ from the two-variable system.
7. Calculate the current $I_{AB}$ using Ohm's Law: $I_{AB} = \frac{V_A - V_B}{6}$.