Question

If $P_r$ is the coefficient of $x^r$ in the expansion of $(1+x)^2\left(1+\frac{x}{2}\right)^2\left(1+\frac{x}{2^2}\right)^2\left(1+\frac{x}{2^3}\right)^2$..., prove that

$P_r = \frac{2^2}{(2^r-1)}(P_{r-1}+P_{r-2})$ and $P_4 = \frac{1072}{315}$.

Answer 1

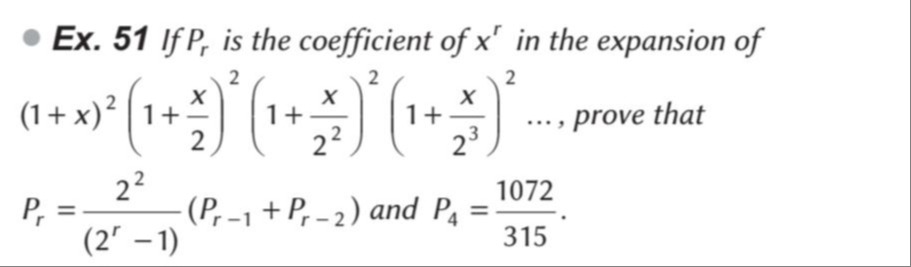
P_r = \frac{2^2}{(2^r-1)}(P_{r-1}+P_{r-2}) \text{ and } P_4 = \frac{1072}{315}

Answer 2

The problem asks us to prove a recurrence relation for the coefficients $P_r$ in the expansion of a given infinite product and then calculate a specific coefficient $P_4$.

Let the given expression be $E(x)$: $E(x) = (1+x)^2\left(1+\frac{x}{2}\right)^2\left(1+\frac{x}{2^2}\right)^2\left(1+\frac{x}{2^3}\right)^2 \dots$ This can be written as an infinite product: $E(x) = \prod_{k=0}^{\infty} \left(1+\frac{x}{2^k}\right)^2$ We observe a functional relationship for $E(x)$. $E(x) = \left(1+\frac{x}{2^0}\right)^2 \prod_{k=1}^{\infty} \left(1+\frac{x}{2^k}\right)^2$ $E(x) = (1+x)^2 \prod_{j=0}^{\infty} \left(1+\frac{x/2}{2^j}\right)^2$ So, $E(x) = (1+x)^2 E(x/2)$.

Let $P_r$ be the coefficient of $x^r$ in the expansion of $E(x)$. We can write $E(x)$ as a power series: $E(x) = \sum_{r=0}^{\infty} P_r x^r$ Substitute this into the functional equation $E(x) = (1+x)^2 E(x/2)$: $\sum_{r=0}^{\infty} P_r x^r = (1+x)^2 \sum_{r=0}^{\infty} P_r \left(\frac{x}{2}\right)^r$ $\sum_{r=0}^{\infty} P_r x^r = (1+2x+x^2) \sum_{r=0}^{\infty} \frac{P_r}{2^r} x^r$ Expand the right side: $\sum_{r=0}^{\infty} P_r x^r = \sum_{r=0}^{\infty} \frac{P_r}{2^r} x^r + 2 \sum_{r=0}^{\infty} \frac{P_r}{2^r} x^{r+1} + \sum_{r=0}^{\infty} \frac{P_r}{2^r} x^{r+2}$ Now, we compare the coefficients of $x^k$ on both sides for $k \ge 2$: $P_k = \frac{P_k}{2^k} + 2 \frac{P_{k-1}}{2^{k-1}} + \frac{P_{k-2}}{2^{k-2}}$ To simplify, multiply the entire equation by $2^k$: $2^k P_k = P_k + 2 \cdot 2 \cdot P_{k-1} + 4 P_{k-2}$ $2^k P_k = P_k + 4 P_{k-1} + 4 P_{k-2}$ Rearrange the terms to solve for $P_k$: $2^k P_k - P_k = 4 P_{k-1} + 4 P_{k-2}$ $(2^k-1)P_k = 4 (P_{k-1} + P_{k-2})$ $P_k = \frac{4}{2^k-1} (P_{k-1} + P_{k-2})$ This proves the first part of the question, as $4=2^2$. So, $P_r = \frac{2^2}{(2^r-1)}(P_{r-1}+P_{r-2})$ is proven.

Next, we need to calculate $P_4$. First, we find the initial coefficients $P_0$ and $P_1$. $P_0$ is the constant term in $E(x)$. Setting $x=0$ in $E(x)$, we get $E(0) = (1)^2(1)^2(1)^2 \dots = 1$. So, $P_0 = 1$. $P_1$ is the coefficient of $x$. $E(x) = (1+2x+x^2)(1+x+x^2/4)(1+x/2+x^2/16)(1+x/4+x^2/64) \dots$ To get $x^1$, we take the $x$ term from one factor and the constant term (1) from all other factors. Coefficient of $x$ from $(1+x)^2$ is $2$. Coefficient of $x$ from $(1+x/2)^2$ is $1$. Coefficient of $x$ from $(1+x/4)^2$ is $1/2$. Coefficient of $x$ from $(1+x/2^k)^2$ is $1/2^{k-1}$. So, $P_1 = 2 + 1 + \frac{1}{2} + \frac{1}{4} + \dots$ This is an infinite geometric series with first term $a=2$ and common ratio $r=1/2$. The sum is $\frac{a}{1-r} = \frac{2}{1-1/2} = \frac{2}{1/2} = 4$. Thus, $P_1 = 4$.

Now, we use the recurrence relation to find $P_2, P_3, P_4$: For $k=2$: $P_2 = \frac{4}{2^2-1}(P_1+P_0) = \frac{4}{3}(4+1) = \frac{4}{3} \cdot 5 = \frac{20}{3}$ For $k=3$: $P_3 = \frac{4}{2^3-1}(P_2+P_1) = \frac{4}{7}\left(\frac{20}{3}+4\right) = \frac{4}{7}\left(\frac{20+12}{3}\right) = \frac{4}{7} \cdot \frac{32}{3} = \frac{128}{21}$ For $k=4$: $P_4 = \frac{4}{2^4-1}(P_3+P_2) = \frac{4}{15}\left(\frac{128}{21}+\frac{20}{3}\right)$ To sum the fractions, find a common denominator (21): $\frac{20}{3} = \frac{20 \cdot 7}{3 \cdot 7} = \frac{140}{21}$. $P_4 = \frac{4}{15}\left(\frac{128}{21}+\frac{140}{21}\right) = \frac{4}{15}\left(\frac{128+140}{21}\right) = \frac{4}{15} \cdot \frac{268}{21}$ $P_4 = \frac{4 \cdot 268}{15 \cdot 21} = \frac{1072}{315}$ This matches the value given in the problem statement.