Solveeit Logo
Login

Question

Question: - **Ex. 48** Prove that $$ { }^{n} C_{3}+{ }^{n} C_{7}+{ }^{n} C_{11}+\ldots=\frac{1}{2}\left\{2^{n-...

  • Ex. 48 Prove that
nC3+nC7+nC11+…=12{2n−1−2n/2sin⁡mπ4}{ }^{n} C_{3}+{ }^{n} C_{7}+{ }^{n} C_{11}+\ldots=\frac{1}{2}\left\{2^{n-1}-2^{n / 2} \sin \frac{m \pi}{4}\right\}
Answer

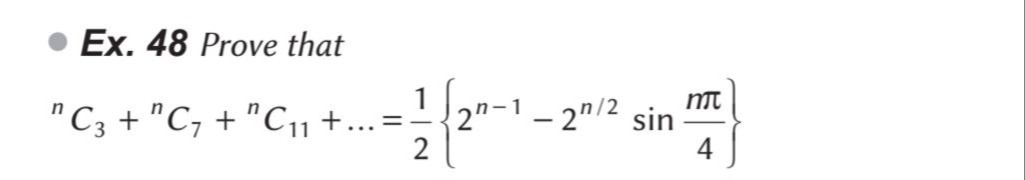
Proved

Explanation

Solution

The problem asks us to prove the identity: nC3+nC7+nC11+…=12{2n−1−2n/2sin⁡nπ4}{ }^{n} C_{3}+{ }^{n} C_{7}+{ }^{n} C_{11}+\ldots=\frac{1}{2}\left\{2^{n-1}-2^{n / 2} \sin \frac{n \pi}{4}\right\} Let the sum be S3S_3. The terms in the sum are binomial coefficients nCk{}^nC_k where k≡3(mod4)k \equiv 3 \pmod 4. This type of sum can be evaluated using the roots of unity, specifically the fourth roots of unity: 1,i,i2=−1,i3=−i1, i, i^2=-1, i^3=-i.

Consider the binomial expansion of (1+x)n(1+x)^n: (1+x)n=nC0+nC1x+nC2x2+nC3x3+…+nCnxn(1+x)^n = { }^{n} C_0 + { }^{n} C_1 x + { }^{n} C_2 x^2 + { }^{n} C_3 x^3 + \ldots + { }^{n} C_n x^n

Let's substitute x=1,−1,i,−ix=1, -1, i, -i:

  1. For x=1x=1: (1+1)n=nC0+nC1+nC2+nC3+…=2n(1+1)^n = { }^{n} C_0 + { }^{n} C_1 + { }^{n} C_2 + { }^{n} C_3 + \ldots = 2^n
  2. For x=−1x=-1: (Valid for n≥1n \ge 1; for n=0n=0, (1−1)0=1(1-1)^0=1) (1−1)n=nC0−nC1+nC2−nC3+…=0(n≥1)(1-1)^n = { }^{n} C_0 - { }^{n} C_1 + { }^{n} C_2 - { }^{n} C_3 + \ldots = 0 \quad (n \ge 1)
  3. For x=ix=i: (1+i)n=nC0+nC1i+nC2i2+nC3i3+nC4i4+…(1+i)^n = { }^{n} C_0 + { }^{n} C_1 i + { }^{n} C_2 i^2 + { }^{n} C_3 i^3 + { }^{n} C_4 i^4 + \ldots (1+i)n=nC0+inC1−nC2−inC3+nC4+…(1+i)^n = { }^{n} C_0 + i{ }^{n} C_1 - { }^{n} C_2 - i{ }^{n} C_3 + { }^{n} C_4 + \ldots Group terms based on the power of ii: (1+i)n=(nC0−nC2+nC4−…)+i(nC1−nC3+nC5−…)(1+i)^n = ({ }^{n} C_0 - { }^{n} C_2 + { }^{n} C_4 - \ldots) + i({ }^{n} C_1 - { }^{n} C_3 + { }^{n} C_5 - \ldots)
  4. For x=−ix=-i: (1−i)n=nC0−nC1i+nC2i2−nC3i3+nC4i4−…(1-i)^n = { }^{n} C_0 - { }^{n} C_1 i + { }^{n} C_2 i^2 - { }^{n} C_3 i^3 + { }^{n} C_4 i^4 - \ldots (1−i)n=nC0−inC1−nC2+inC3+nC4−…(1-i)^n = { }^{n} C_0 - i{ }^{n} C_1 - { }^{n} C_2 + i{ }^{n} C_3 + { }^{n} C_4 - \ldots Group terms based on the power of ii: (1−i)n=(nC0−nC2+nC4−…)−i(nC1−nC3+nC5−…)(1-i)^n = ({ }^{n} C_0 - { }^{n} C_2 + { }^{n} C_4 - \ldots) - i({ }^{n} C_1 - { }^{n} C_3 + { }^{n} C_5 - \ldots)

Let Sk=∑j=0⌊(n−k)/4⌋nC4j+kS_k = \sum_{j=0}^{\lfloor (n-k)/4 \rfloor} {}^{n}C_{4j+k} for k=0,1,2,3k=0,1,2,3. So, S0=nC0+nC4+nC8+…S_0 = { }^{n} C_0 + { }^{n} C_4 + { }^{n} C_8 + \ldots S1=nC1+nC5+nC9+…S_1 = { }^{n} C_1 + { }^{n} C_5 + { }^{n} C_9 + \ldots S2=nC2+nC6+nC10+…S_2 = { }^{n} C_2 + { }^{n} C_6 + { }^{n} C_{10} + \ldots S3=nC3+nC7+nC11+…S_3 = { }^{n} C_3 + { }^{n} C_7 + { }^{n} C_{11} + \ldots (This is the sum we need to find)

From the expansions above:

  1. S0+S1+S2+S3=2nS_0 + S_1 + S_2 + S_3 = 2^n (Eq. A)
  2. S0−S1+S2−S3=0(n≥1)S_0 - S_1 + S_2 - S_3 = 0 \quad (n \ge 1) (Eq. B)
  3. (1+i)n=(S0−S2)+i(S1−S3)(1+i)^n = (S_0 - S_2) + i(S_1 - S_3) (Eq. C)
  4. (1−i)n=(S0−S2)−i(S1−S3)(1-i)^n = (S_0 - S_2) - i(S_1 - S_3) (Eq. D)

From (Eq. A) and (Eq. B): Adding (Eq. A) and (Eq. B): 2(S0+S2)=2n  ⟹  S0+S2=2n−12(S_0 + S_2) = 2^n \implies S_0 + S_2 = 2^{n-1} (Eq. E) Subtracting (Eq. B) from (Eq. A): 2(S1+S3)=2n  ⟹  S1+S3=2n−12(S_1 + S_3) = 2^n \implies S_1 + S_3 = 2^{n-1} (Eq. F)

Now, express (1+i)n(1+i)^n and (1−i)n(1-i)^n in polar form using De Moivre's Theorem. 1+i=12+12(cos⁡(π/4)+isin⁡(π/4))=2eiπ/41+i = \sqrt{1^2+1^2} (\cos(\pi/4) + i \sin(\pi/4)) = \sqrt{2} e^{i\pi/4} 1−i=12+(−1)2(cos⁡(−π/4)+isin⁡(−π/4))=2e−iπ/41-i = \sqrt{1^2+(-1)^2} (\cos(-\pi/4) + i \sin(-\pi/4)) = \sqrt{2} e^{-i\pi/4}

So, (1+i)n=(2)n(cos⁡(nπ/4)+isin⁡(nπ/4))=2n/2cos⁡(nπ/4)+i2n/2sin⁡(nπ/4)(1+i)^n = (\sqrt{2})^n (\cos(n\pi/4) + i \sin(n\pi/4)) = 2^{n/2} \cos(n\pi/4) + i 2^{n/2} \sin(n\pi/4) (Eq. G) (1−i)n=(2)n(cos⁡(−nπ/4)+isin⁡(−nπ/4))=2n/2cos⁡(nπ/4)−i2n/2sin⁡(nπ/4)(1-i)^n = (\sqrt{2})^n (\cos(-n\pi/4) + i \sin(-n\pi/4)) = 2^{n/2} \cos(n\pi/4) - i 2^{n/2} \sin(n\pi/4) (Eq. H)

Comparing the real and imaginary parts of (Eq. C) with (Eq. G): S0−S2=2n/2cos⁡(nπ/4)S_0 - S_2 = 2^{n/2} \cos(n\pi/4) (Eq. I) S1−S3=2n/2sin⁡(nπ/4)S_1 - S_3 = 2^{n/2} \sin(n\pi/4) (Eq. J)

We need to find S3S_3. We have a system of two equations involving S1S_1 and S3S_3:

  1. S1+S3=2n−1S_1 + S_3 = 2^{n-1} (from Eq. F)
  2. S1−S3=2n/2sin⁡(nπ/4)S_1 - S_3 = 2^{n/2} \sin(n\pi/4) (from Eq. J)

Subtracting the second equation from the first: (S1+S3)−(S1−S3)=2n−1−2n/2sin⁡(nπ/4)(S_1 + S_3) - (S_1 - S_3) = 2^{n-1} - 2^{n/2} \sin(n\pi/4) 2S3=2n−1−2n/2sin⁡(nπ/4)2S_3 = 2^{n-1} - 2^{n/2} \sin(n\pi/4) S3=12{2n−1−2n/2sin⁡(nπ4)}S_3 = \frac{1}{2} \left\{ 2^{n-1} - 2^{n/2} \sin\left(\frac{n\pi}{4}\right) \right\}

This proof is valid for n≥1n \ge 1. For n=0n=0, the sum is 0, but the formula gives 1/41/4. However, the sum is usually considered for n≥1n \ge 1 when terms like nCk{}^nC_k are defined. The problem itself implies n≥3n \ge 3 for nC3{}^nC_3 to be the first non-zero term.

The final answer is Proved\boxed{\text{Proved}}

Explanation of the solution: The sum of binomial coefficients nCk{}^nC_k where kk follows an arithmetic progression with a common difference of 4 (i.e., k≡r(mod4)k \equiv r \pmod 4) can be found using the properties of the fourth roots of unity.

  1. Write out the binomial expansion of (1+x)n(1+x)^n.
  2. Substitute x=1,−1,i,−ix=1, -1, i, -i into the expansion.
  3. Group the terms based on the remainder of the index kk when divided by 4, creating sums S0,S1,S2,S3S_0, S_1, S_2, S_3.
  4. Express (1+i)n(1+i)^n and (1−i)n(1-i)^n in polar form using De Moivre's Theorem.
  5. Equate the real and imaginary parts of the complex expressions with the sums SkS_k.
  6. Solve the resulting system of linear equations for $S_3.

Subject: Mathematics Chapter: Binomial Theorem Topic: Properties of Binomial Coefficients / Sums of Binomial Coefficients Difficulty Level: Medium Question Type: Descriptive