Question
Question: Solve the following inequality: \(||2x+3|-4| \le 10\)...
Solve the following inequality:
∣∣2x+3∣−4∣≤10
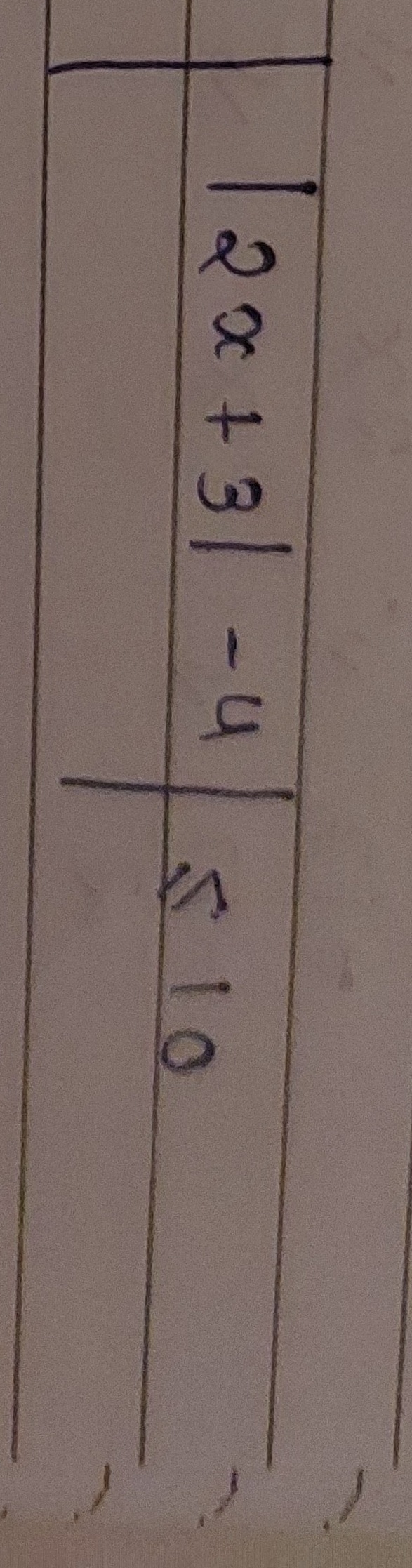
[−217,211]
Solution
The given inequality is ∣∣2x+3∣−4∣≤10.
We use the property that for any expression A and a non-negative number B, the inequality ∣A∣≤B is equivalent to −B≤A≤B.
Applying this property to the given inequality, where A=∣2x+3∣−4 and B=10, we get: −10≤∣2x+3∣−4≤10
Now, we solve this compound inequality for ∣2x+3∣. Add 4 to all parts of the inequality: −10+4≤∣2x+3∣−4+4≤10+4 −6≤∣2x+3∣≤14
This compound inequality can be split into two separate inequalities:
- ∣2x+3∣≥−6
- ∣2x+3∣≤14
Let's solve the first inequality, ∣2x+3∣≥−6. The absolute value of any real number is always non-negative, i.e., ∣y∣≥0 for any real number y. Since 0≥−6, the inequality ∣2x+3∣≥−6 is true for all real values of x. The solution set for this inequality is R.
Now, let's solve the second inequality, ∣2x+3∣≤14. Using the property ∣A∣≤B⟺−B≤A≤B again, where A=2x+3 and B=14, we get: −14≤2x+3≤14
Now, we solve this compound inequality for x. Subtract 3 from all parts: −14−3≤2x+3−3≤14−3 −17≤2x≤11
Now, divide all parts by 2: 2−17≤22x≤211 −217≤x≤211
The solution set for this inequality is the interval [−217,211].
The solution to the original inequality is the intersection of the solution sets of the two separate inequalities. The intersection of R and [−217,211] is [−217,211].
Therefore, the solution set for the inequality ∣∣2x+3∣−4∣≤10 is x∈[−217,211].
